hacker-laws-website

💻📖 prawa-hakerskie

Prawa, teorie, zasady i wzorce, które programiści uznają za przydatne.

Tłumaczenia: 🇮🇩 🇧🇷 🇨🇳 🇩🇪 🇫🇷 🇬🇷 🇮🇹 🇱🇻 🇰🇷 🇵🇱 🇷🇺 🇪🇸 🇹🇷 🇯🇵 🇺🇦

Podoba Ci się ten projekt? Proszę rozważyć sponsorowanie mnie i tłumaczy . Sprawdź również ten podcast na The Changelog - Laws for Hackers to Live By, aby dowiedzieć się więcej o projekcie! Możesz także pobrać najnowszy e-book w formacie PDF . Sprawdź Przewodnik dla twórców, jeśli chcesz wnieść swój wkład!

Wstęp

Istnieje wiele praw, o których ludzie dyskutują, mówiąc o rozwoju. To repozytorium jest odniesieniem i przeglądem niektórych z najczęstszych. Podziel się i prześlij PR!

Odpowiedź: To repozytorium zawiera wyjaśnienie niektórych praw, zasad i wzorców, ale nie zaleca żadnego z nich. To, czy należy je zastosować, zawsze będzie kwestią dyskusyjną i w dużej mierze zależy od tego, nad czym pracujesz.

Prawa

No to zaczynamy!

Zasada 90-9-1 (zasada 1%)

Reguła 1% na Wikipedii

Zasada 90-9-1 sugeruje, że w społeczności internetowej, takiej jak wiki, 90% uczestników tylko korzysta z treści, 9% edytuje lub modyfikuje treść, a 1% uczestników dodaje treść.

Przykłady ze świata rzeczywistego:

Zobacz też:

Prawo Amdahla

Prawo Amdahla na Wikipedii

Prawo Amdahla to wzór pokazujący potencjalne przyspieszenie zadania obliczeniowego, które można osiągnąć zwiększając zasoby systemu. Zwykle używany w obliczeniach równoległych, może przewidzieć rzeczywiste korzyści ze zwiększenia liczby procesorów, co jest ograniczone przez możliwość równoległości programu.

Najlepiej zilustrowane przykładem. Jeśli program składa się z dwóch części, części A, która musi być wykonywana przez pojedynczy procesor, i części B, która może być zrównoleglona, to widzimy, że dodanie wielu procesorów do systemu wykonującego program może mieć tylko ograniczoną korzyść . Potencjalnie może znacznie poprawić prędkość części B - ale prędkość części A pozostanie niezmieniona.

Poniższy diagram pokazuje kilka przykładów potencjalnej poprawy szybkości:

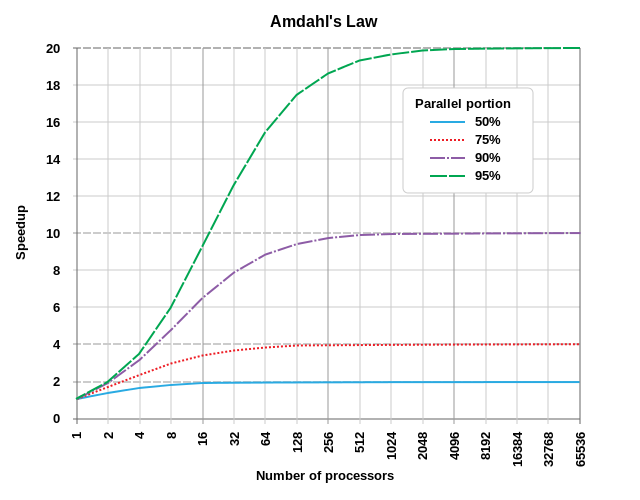
Schemat: Prawo Amdahla

(Odniesienie do obrazu: Daniels219 z angielskiej Wikipedii, Creative Commons Attribution-Share Alike 3.0 Unported, https://en.wikipedia.org/wiki/File:AmdahlsLaw.svg)

Jak widać, nawet program, który można zrównoleglać w 50%, przyniesie niewiele korzyści poza 10 jednostkami przetwarzania, podczas gdy program, który można zrównolelizować w 95%, nadal może osiągnąć znaczną poprawę szybkości przy ponad tysiącu jednostek przetwarzania.

Ponieważ prawo Moore’a zwalnia, a przyspieszenie szybkości poszczególnych procesorów zwalnia, równoległość jest kluczem do poprawy wydajności. Programowanie graficzne jest doskonałym przykładem - przy nowoczesnych obliczeniach opartych na Shader, pojedyncze piksele lub fragmenty mogą być renderowane równolegle - dlatego współczesne karty graficzne często mają wiele tysięcy rdzeni przetwarzających (GPU lub Shader Units).

Zobacz też:

Teoria zepsutych okien

Teoria rozbitycg okien na Wikipedii

Teoria rozbitych okien sugeruje, że widoczne oznaki przestępczości (lub braku dbałości o środowisko) prowadzą do kolejnych i poważniejszych przestępstw (lub dalszego pogorszenia stanu środowiska).

Teoria ta została zastosowana do rozwoju oprogramowania, co sugeruje, że kod niskiej jakości (lub dług techniczny ) może prowadzić do przekonania, że wysiłki na rzecz poprawy jakości mogą być ignorowane lub niedoceniane, co prowadzi do dalszej złej jakości kodu. Ten efekt kaskadowo prowadzi do znacznego spadku jakości z biegiem czasu.

Zobacz też:

Przykłady:

Prawo Brooksa

Prawo Brooksa na Wikipedii

Dodanie zasobów ludzkich do spóźnionego projektu rozwoju oprogramowania sprawia, że jest to później.

Prawo to sugeruje, że w wielu przypadkach próba przyspieszenia realizacji projektu, który jest już spóźniony, poprzez dodanie większej liczby osób, spowoduje, że realizacja będzie jeszcze późniejsza. Brooks nie ma wątpliwości, że jest to nadmierne uproszczenie, jednak ogólne rozumowanie jest takie, że biorąc pod uwagę czas narastania nowych zasobów i ogólne koszty komunikacji, w krótkim czasie prędkość spada. Ponadto wiele zadań może nie być podzielnych, tj. łatwo rozdzielonych między więcej zasobów, co oznacza, że potencjalny wzrost prędkości jest również mniejszy.

Powszechne zdanie przy porodzie „Dziewięć kobiet nie może spłodzić dziecka w ciągu jednego miesiąca” odnosi się do prawa Brooksa, w szczególności do faktu, że niektóre rodzaje pracy nie są podzielne ani równoległe.

Jest to tematem przewodnim książki „ Miesiąc mitycznego człowieka ”.

Zobacz też:

Twierdzenie CAP (Twierdzenie Brewera)

Twierdzenie CAP (zdefiniowane przez Erica Brewera) stwierdza, że w przypadku rozproszonego magazynu danych można uzyskać tylko dwie z trzech następujących gwarancji (co najwyżej):

Sedno rozumowania jest następujące. Nie można zagwarantować, że partycja sieciowa nie wystąpi (zobacz The Fallacies of Distributed Computing ). Dlatego w przypadku partycji możemy albo anulować operację (zwiększając spójność i zmniejszając dostępność) albo kontynuować (zwiększając dostępność, ale zmniejszając spójność).

Nazwa pochodzi od pierwszych liter gwarancji (spójność, dostępność, tolerancja partycji). Należy pamiętać, że bardzo ważne jest, aby mieć świadomość, że nie dotyczy to ACID , który ma inną definicję spójności. Niedawno opracowano twierdzenie PACELC, które dodaje ograniczenia dotyczące opóźnień i spójności, gdy sieć nie jest podzielona na partycje (tj. gdy system działa zgodnie z oczekiwaniami).

Większość nowoczesnych platform bazodanowych potwierdza to twierdzenie pośrednio, oferując użytkownikowi bazy danych opcję wyboru między operacją o wysokiej dostępności (która może obejmować „brudny odczyt”) a operacją wysoce spójną (na przykład „zapis z potwierdzeniem kworum ‘).

Przykłady ze świata rzeczywistego:

Zobacz też:

Prawo Conwaya

Prawo Conwaya na Wikipedii

Prawo to sugeruje, że granice techniczne systemu będą odzwierciedlać strukturę organizacji. Często mówi się o tym, gdy patrzymy na ulepszenia organizacji. Prawo Conwaya sugeruje, że jeśli organizacja jest podzielona na wiele małych, niepowiązanych ze sobą jednostek, tak będzie tworzone oprogramowanie. Jeśli organizacja jest zbudowana bardziej wokół „branż”, które są zorientowane na funkcje lub usługi, systemy oprogramowania również to odzwierciedlą.

Zobacz też:

Prawo Cunninghama

Prawo Cunninghama na Wikipedii

Najlepszym sposobem na uzyskanie prawidłowej odpowiedzi w Internecie nie jest zadawanie pytań, ale zamieszczenie błędnej odpowiedzi.

Według Stevena McGeady’ego Ward Cunningham poradził mu na początku lat 80.: „Najlepszym sposobem na uzyskanie prawidłowej odpowiedzi w Internecie jest nie zadawanie pytań, ale zamieszczenie złej odpowiedzi”. McGeady nazwał to prawo Cunninghama, chociaż Cunningham zaprzecza własności, nazywając to „błędem”. Chociaż pierwotnie odnosiło się do interakcji w Usenecie, prawo zostało użyte do opisania działania innych społeczności internetowych (np. Wikipedia, Reddit, Twitter, Facebook).

Zobacz też:

Numer Dunbara

Numer Dunbara na Wikipedii

„Liczba Dunbara jest sugerowanym limitem poznawczym liczby osób, z którymi można utrzymywać stabilne relacje społeczne – relacje, w których jednostka wie, kim jest każda osoba i jak każda osoba odnosi się do każdej innej osoby”. Istnieje pewna niezgodność co do dokładnej liczby. „… [Dunbar] zaproponował, że ludzie mogą wygodnie utrzymywać tylko 150 stabilnych związków”. Umieścił tę liczbę w bardziej społecznym kontekście, „liczbę osób, których nie czulibyście się zawstydzeni dołączeniem do nieproszonych drinków, gdybyście wpadli na nich w barze”. Szacunki dotyczące liczby wahają się od 100 do 250.

Podobnie jak w przypadku stabilnych relacji między jednostkami, utrzymanie relacji programisty z bazą kodu wymaga wysiłku. W obliczu dużych, skomplikowanych projektów lub posiadania wielu projektów opieramy się na konwencji, zasadach i modelowanych procedurach w celu skalowania. Liczba Dunbar jest ważna nie tylko w miarę rozwoju biura, ale także przy ustalaniu zakresu działań zespołu lub decydowaniu, kiedy system powinien zainwestować w narzędzia, które pomogą w modelowaniu i automatyzacji ogólnych kosztów logistycznych. Umieszczając liczbę w kontekście inżynierskim, jest to liczba projektów (lub znormalizowana złożoność pojedynczego projektu), w przypadku których możesz czuć się pewnie, dołączając do rotacji na wezwanie, aby wesprzeć.

Zobacz też:

Efekt Dunninga-Krugera

Efekt Dunninga-Krugera na Wikipedii

Jeśli jesteś niekompetentny, nie możesz wiedzieć, że jesteś niekompetentny… Umiejętności potrzebne do uzyskania prawidłowej odpowiedzi to dokładnie te umiejętności, których potrzebujesz, aby rozpoznać, jaka jest właściwa odpowiedź.

( Dawid Dunning )

Efekt Dunninga-Krugera to teoretyczne zniekształcenie poznawcze, które zostało opisane przez Davida Dunninga i Justina Krugera w badaniu psychologicznym i artykule z 1999 roku. Badanie sugeruje, że osoby o niskim poziomie umiejętności w zadaniu prawdopodobnie przeceniają swoją zdolność do zadania. Proponowaną przyczyną tego nastawienia jest to, że wymagana jest wystarczająca świadomość złożoności problemu lub dziedziny, aby osoba była w stanie wyrobić sobie świadomą opinię na temat swojej zdolności do pracy w tej dziedzinie.

Efekt Dunninga-Krugera był czasami używany do opisania powiązanego, ale niekoniecznie dorozumianego efektu, który można opisać jako „Im mniej dana osoba rozumie daną dziedzinę, tym bardziej prawdopodobne jest, że uwierzy, że może łatwo rozwiązać problemy w tej dziedzinie, ponieważ są bardziej skłonni do postrzegania domeny jako prostej ”. Ten bardziej ogólny efekt jest bardzo istotny w technologii. Sugerowałoby to, że ludzie mniej zaznajomieni z daną domeną, na przykład nietechniczni członkowie zespołu lub mniej doświadczeni członkowie zespołu, częściej nie doceniają wysiłku wymaganego do rozwiązania problemu w tej przestrzeni.

Wraz ze wzrostem zrozumienia i doświadczenia danej osoby w danej domenie, może ona napotkać inny efekt, który polega na tym, że mają tendencję do przeceniania zdolności innych lub niedoceniania własnych zdolności, ponieważ są tak doświadczeni w tej domenie. We wszystkich przypadkach skutki te są zniekształceniami poznawczymi . Podobnie jak w przypadku każdego uprzedzenia, zrozumienie, że może ono być obecne, często wystarczy, aby uniknąć wyzwań – ponieważ gdy istnieje świadomość uprzedzenia, można uwzględnić więcej danych wejściowych i opinii, aby spróbować wyeliminować te uprzedzenia. Ściśle pokrewnym jest nastawienie iluzorycznej wyższości .

Przykłady ze świata rzeczywistego:

Prawo Fittsa

Prawo Fittsa na Wikipedii

Prawo Fittsa przewiduje, że czas potrzebny do przemieszczenia się do obszaru docelowego jest funkcją odległości do celu podzielonej przez szerokość celu.

Schemat: Prawo dopasowania

(Odniesienie do obrazu: Foobar628 z angielskiej Wikipedii, Creative Commons Attribution-Share Alike 3.0 Unported, https://en.wikipedia.org/wiki/Fitts%27s_law#/media/File:Fitts_Law.svg)

Konsekwencje tego prawa nakazują, aby przy projektowaniu UX czy UI elementy interaktywne były jak największe, a odległość między obszarem uwagi użytkownika a elementem interaktywnym była jak najmniejsza. Ma to konsekwencje dla projektu, takie jak grupowanie zadań, które są często używane blisko siebie.

Formalizuje również koncepcję „magicznych rogów”, rogów ekranu, do których użytkownik może „przesuwać” myszą, aby łatwo trafić – czyli tam, gdzie można umieścić kluczowe elementy interfejsu użytkownika. Przycisk Start systemu Windows znajduje się w magicznym rogu, co ułatwia wybór, a jako interesujący kontrast, przycisk „zamknij okno” systemu MacOS nie znajduje się w magicznym rogu, co utrudnia przypadkowe trafienie.

Zobacz też:

Prawo Galla

Prawo Galla na Wikipedii

Niezmiennie okazuje się, że złożony system, który działa, wyewoluował z prostego systemu, który działał. Złożony system zaprojektowany od podstaw nigdy nie działa i nie można go załatać, aby działał. Musisz zacząć od nowa z działającym prostym systemem.

( John Gall )

Prawo Galla sugeruje, że próby zaprojektowania bardzo złożonych systemów mogą się nie powieść. Bardzo złożone systemy rzadko są budowane za jednym razem, ale zamiast tego ewoluują z prostszych systemów.

Klasycznym przykładem jest sieć ogólnoświatowa. W obecnym stanie jest to bardzo złożony system. Jednak początkowo został zdefiniowany jako prosty sposób udostępniania treści między instytucjami akademickimi. Odniósł duży sukces w realizacji tych celów i z czasem ewoluował, by stać się bardziej złożony.

Zobacz też:

Prawo Goodharta

Prawo Goodharta na Wikipedii

Jakakolwiek zaobserwowana prawidłowość statystyczna będzie miała tendencję do załamania się, gdy zostanie na nią nałożona presja w celach kontrolnych.

Karola Goodharta

Również powszechnie określany jako:

Kiedy miara staje się celem, przestaje być dobrą miarą.

Marilyn Strathern

Prawo stanowi, że optymalizacje oparte na pomiarach mogą prowadzić do dewaluacji samego wyniku pomiaru. Nadmiernie selektywny zestaw miar ( KPI ) zastosowany na ślepo do procesu powoduje zniekształcony efekt. Ludzie mają tendencję do optymalizacji lokalnie, „ogrywając” system w celu spełnienia określonych wskaźników, zamiast zwracać uwagę na całościowy wynik swoich działań.

Przykłady ze świata rzeczywistego:

Zobacz też:

Brzytwa Hanlona

Brzytwa Hanlona na Wikipedii

Nigdy nie przypisuj złośliwości tego, co adekwatnie tłumaczy się głupotą.

Robert J. Hanlon

Zasada ta sugeruje, że działania prowadzące do negatywnych skutków nie były wynikiem złej woli. Zamiast tego negatywny wynik jest bardziej prawdopodobnie przypisywany tym działaniom i/lub wpływowi, który nie jest w pełni zrozumiały.

Prawo Hicka (Prawo Hicka-Hymana)

Prawo Hicka na Wikipedii

Czas podejmowania decyzji rośnie logarytmicznie wraz z liczbą opcji do wyboru.

William Edmund Hick i Ray Hyman

W poniższym równaniu T to czas na podjęcie decyzji, n to liczba opcji, a b to stała określona na podstawie analizy danych.

Prawo Hicksa

(Odniesienie do obrazu: Creative Commons Attribution-Share Alike 3.0 Unported, https://en.wikipedia.org/wiki/Hick%27s_law)

To prawo ma zastosowanie tylko wtedy, gdy liczba opcji jest uporządkowana , na przykład alfabetycznie. Jest to implikowane w logarytmie o podstawie dwa, co oznacza, że osoba podejmująca decyzje zasadniczo przeprowadza wyszukiwanie binarne . Jeśli opcje nie są dobrze uporządkowane, eksperymenty pokazują, że czas potrzebny jest liniowy.

Ma to znaczący wpływ na projektowanie interfejsu użytkownika; zapewnienie, że użytkownicy mogą łatwo przeszukiwać opcje, prowadzi do szybszego podejmowania decyzji.

W prawie Hicka wykazano również korelację między IQ a czasem reakcji, jak pokazano w Speed of Information Processing: Developmental Change and Links to Intelligence .

Zobacz też:

Prawo Hofstadtera

Prawo Hofstadtera na Wikipedii

Zawsze trwa to dłużej niż się spodziewasz, nawet biorąc pod uwagę prawo Hofstadtera.

(Douglas Hofstadter)

Możesz usłyszeć to prawo, o którym mowa, patrząc na szacunki, jak długo coś potrwa. Wydaje się truizmem w tworzeniu oprogramowania, że nie jesteśmy zbyt dobrzy w dokładnym szacowaniu, ile czasu zajmie dostarczenie czegoś.

To jest z książki ‘ Gödel, Escher, Bach: Wieczny złoty warkocz ‘.

Zobacz też:

Prawo Hutbera

Prawo Hutbera na Wikipedii

Poprawa oznacza pogorszenie.

( Patryk Hutber )

To prawo sugeruje, że ulepszenia systemu doprowadzą do pogorszenia innych części lub ukryją inne pogorszenie, prowadząc ogólnie do degradacji obecnego stanu systemu.

Na przykład, zmniejszenie opóźnienia odpowiedzi dla określonego punktu końcowego może spowodować dalsze problemy z przepustowością i pojemnością w przepływie żądań, wpływając na zupełnie inny podsystem.

Cykl szumu i prawo Amary

Cykl szumu na Wikipedii

Mamy tendencję do przeceniania wpływu technologii na krótką metę i niedoceniania jej na dłuższą metę.

(Roy Amara)

Hype Cycle to wizualna reprezentacja ekscytacji i rozwoju technologii na przestrzeni czasu, pierwotnie wyprodukowana przez firmę Gartner. Najlepiej pokazać to za pomocą wizualizacji:

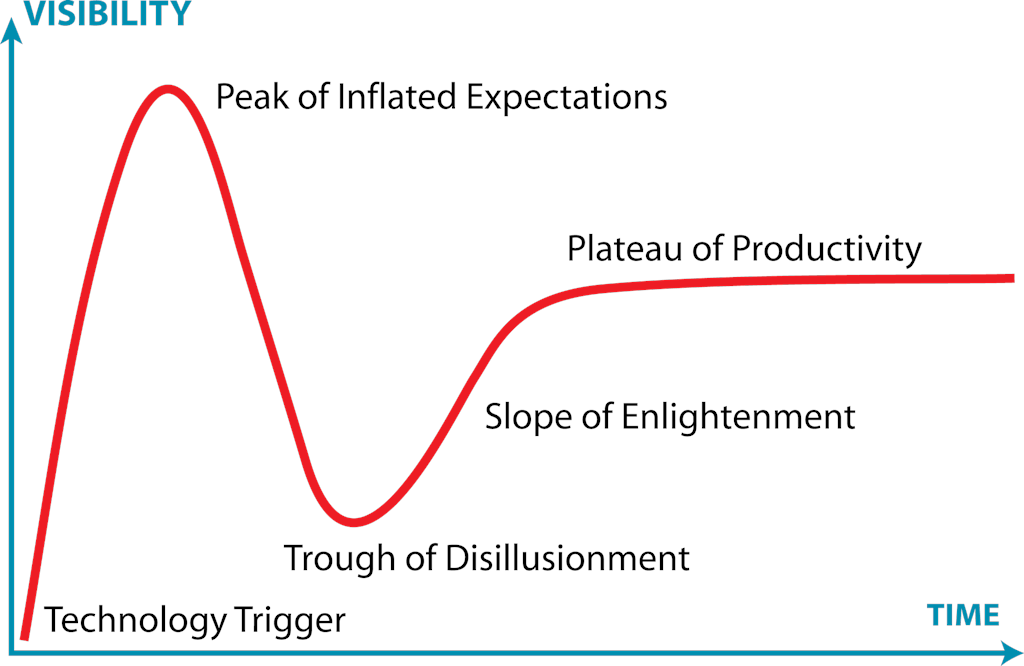
Cykl szumu

(Odniesienie do obrazu: Jeremykemp z angielskiej Wikipedii, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10547051)

Krótko mówiąc, ten cykl sugeruje, że nowa technologia i jej potencjalny wpływ zwykle budzi ogromne zainteresowanie. Zespoły często szybko wskakują w te technologie i czasami są rozczarowane wynikami. Może to być spowodowane tym, że technologia nie jest jeszcze wystarczająco dojrzała lub aplikacje w świecie rzeczywistym nie są jeszcze w pełni zrealizowane. Po pewnym czasie zwiększają się możliwości technologii i praktyczne możliwości jej wykorzystania, a zespoły mogą wreszcie stać się produktywne. Cytat Roya Amary podsumowuje to w najbardziej zwięzły sposób: „Mamy tendencję do przeceniania wpływu technologii na krótką metę i niedoceniania na dłuższą metę”.

Prawo Hyruma (prawo niejawnych interfejsów)

Prawo Hyruma w Internecie

Przy wystarczającej liczbie użytkowników API nie ma znaczenia, co obiecujesz w kontrakcie: wszystkie obserwowalne zachowania Twojego systemu będą przez kogoś zależne.

(Hyrum Wright)

Prawo Hyrum stanowi, że gdy masz wystarczająco dużą liczbę konsumentów API, wszystkie zachowania API (nawet te, które nie są zdefiniowane jako część umowy publicznej) w końcu staną się przez kogoś zależne. Trywialnym przykładem mogą być elementy niefunkcjonalne, takie jak czas odpowiedzi API. Bardziej subtelnym przykładem mogą być konsumenci, którzy polegają na zastosowaniu wyrażenia regularnego do komunikatu o błędzie w celu określenia typu błędu interfejsu API. Nawet jeśli kontrakt publiczny interfejsu API nie mówi nic o zawartości komunikatu, wskazując, że użytkownicy powinni użyć powiązanego kodu błędu, niektórzy użytkownicy mogą korzystać z komunikatu, a zmiana komunikatu zasadniczo przerywa interfejs API dla tych użytkowników.

Zobacz też:

Prawo Kernighana

Debugowanie jest dwa razy trudniejsze niż pisanie kodu. Dlatego, jeśli piszesz kod tak sprytnie, jak to tylko możliwe, z definicji nie jesteś wystarczająco sprytny, aby go debugować.

(Brian Kernighan)

Prawo Kernighana zostało nazwane na cześć Briana Kernighana i pochodzi z cytatu z książki Kernighana i Plaugera „ Elementy stylu programowania” :

Każdy wie, że debugowanie jest dwa razy trudniejsze niż pisanie programu. Więc jeśli jesteś tak sprytny, jak potrafisz, kiedy to piszesz, jak możesz to kiedykolwiek debugować?

Choć hiperboliczne, prawo Kernighana przedstawia argument, że prosty kod ma być lepszy od kodu złożonego, ponieważ debugowanie wszelkich problemów pojawiających się w kodzie złożonym może być kosztowne lub nawet niemożliwe.

Zobacz też:

Prawo Linusa

Prawo Linusa na Wikipedii

Biorąc pod uwagę wystarczającą liczbę gałek ocznych, wszystkie błędy są płytkie.

Eric S. Raymond

To prawo po prostu mówi, że im więcej ludzi widzi problem, tym większe prawdopodobieństwo, że ktoś już wcześniej widział i rozwiązał problem lub coś bardzo podobnego.

Chociaż pierwotnie był używany do opisywania wartości modeli open-source dla projektów, może być zaakceptowany dla każdego rodzaju projektu oprogramowania. Można go również rozszerzyć na procesy - więcej przeglądów kodu, więcej statycznej analizy i wielobranżowe procesy testowe sprawią, że problemy będą bardziej widoczne i łatwiejsze do zidentyfikowania.

Bardziej formalnym oświadczeniem może być:

Mając wystarczająco dużą bazę beta-testerów i programistów, prawie każdy problem zostanie szybko scharakteryzowany i może zostać rozwiązany przez kogoś, kto już wcześniej spotkał się z podobnym problemem.

Prawo to zostało nazwane na cześć Linusa Torvaldsa w książce Erica S. Raymonda „ Katedra i bazar ”.

Prawo Metcalfego

Prawo Metcalfe’a na Wikipedii

W teorii sieci wartość systemu rośnie w przybliżeniu do kwadratu liczby użytkowników systemu.

Prawo to opiera się na liczbie możliwych połączeń parami w systemie i jest ściśle związane z prawem Reeda . Odlyzko i inni argumentowali, że zarówno prawo Reeda, jak i prawo Metcalfe’a zawyżają wartość systemu, nie uwzględniając granic ludzkiego poznania na efektach sieciowych; zobacz Numer Dunbara .

Zobacz też:

prawo Moore’a

Prawo Moore’a na Wikipedii

Liczba tranzystorów w układzie scalonym podwaja się mniej więcej co dwa lata.

Prognozy Moore’a, często używane do zilustrowania szybkości, z jaką poprawiła się technologia półprzewodników i chipów, okazały się bardzo dokładne w okresie od lat 70. do późnych lat 2000. W ostatnich latach trend nieznacznie się zmienił, częściowo ze względu na fizyczne ograniczenia dotyczące stopnia miniaturyzacji komponentów . Jednak postępy w zrównoleglaniu i potencjalnie rewolucyjne zmiany w technologii półprzewodnikowej i obliczeniach kwantowych mogą oznaczać, że prawo Moore’a może nadal obowiązywać przez dziesięciolecia.

Prawo Murphy’ego / Prawo Soda

Prawo Murphy’ego na Wikipedii

Wszystko, co może pójść nie tak, pójdzie nie tak.

Powiązane z Edwardem A. Murphym, Jr Murphy’s Law stwierdza, że jeśli coś może pójść nie tak, to pójdzie nie tak.

To powszechne powiedzenie wśród programistów. Czasami nieoczekiwane dzieje się podczas tworzenia, testowania, a nawet produkcji. Może to być również związane z (bardziej powszechnym w brytyjskim angielskim) Prawie Soda :

Jeśli coś może pójść nie tak, to w najgorszym możliwym momencie.

Te „prawa” są na ogół używane w komicznym sensie. Jednak zjawiska takie jak błąd potwierdzenia i błąd selekcji mogą skłaniać ludzi do nadmiernego podkreślania tych praw (w większości przypadków, gdy coś działa, pozostają niezauważone, jednak niepowodzenia są bardziej zauważalne i wywołują więcej dyskusji).

Zobacz też:

Brzytwa Ockhama

Brzytwa Ockhama na Wikipedii

Nie należy mnożyć jednostek bez konieczności.

Wilhelm z Ockhama

Brzytwa Ockhama mówi, że spośród kilku możliwych rozwiązań najbardziej prawdopodobnym rozwiązaniem jest to, które ma najmniejszą liczbę koncepcji i założeń. To rozwiązanie jest najprostsze i rozwiązuje tylko zadany problem, bez wprowadzania przypadkowych złożoności i ewentualnych negatywnych konsekwencji.

Zobacz też:

Przykład:

Prawo Parkinsona

Prawo Parkinsona na Wikipedii

Praca rozwija się tak, aby wypełnić czas dostępny na jej wykonanie.

W swoim pierwotnym kontekście ustawa ta opierała się na badaniach biurokracji. Można to pesymistycznie zastosować do inicjatyw rozwoju oprogramowania, zgodnie z teorią, że zespoły będą nieefektywne do czasu, gdy zbliżają się terminy, a następnie spieszą się, aby ukończyć pracę w terminie, co sprawia, że rzeczywisty termin jest nieco arbitralny.

Gdyby to prawo zostało połączone z prawem Hofstadtera , osiągnięto jeszcze bardziej pesymistyczny punkt widzenia - praca rozszerzy się, aby wypełnić czas dostępny na jej ukończenie i nadal będzie trwać dłużej niż oczekiwano .

Zobacz też:

Przedwczesny efekt optymalizacji

Przedwczesna optymalizacja na WikiWikiWeb

Przedwcześnie optymalizacja jest źródłem wszelkiego zła.

(Donald Knuth)

W artykule Donald Knuth’s Structured Programming with Go To Statements napisał: „Programiści marnują ogromne ilości czasu na myślenie lub martwienie się o szybkość niekrytycznych części swoich programów, a te próby wydajności mają naprawdę silny negatywny wpływ podczas debugowania i konserwacja są brane pod uwagę. Powinniśmy zapomnieć o małych wydajnościach, powiedzmy w 97% przypadków: przedwczesna optymalizacja jest źródłem wszelkiego zła . Jednak nie powinniśmy przepuszczać naszych możliwości w tych krytycznych 3%.”

Jednak przedwczesną optymalizację można zdefiniować (w mniej obciążonych terminach) jako optymalizację, zanim zorientujemy się, że jest to konieczne.

Prawo Putta

Prawo Putta na Wikipedii

Technologia jest zdominowana przez dwa typy ludzi, tych, którzy rozumieją to, czym nie zarządzają, i tych, którzy zarządzają tym, czego nie rozumieją.

Po prawie Putta często następuje następstwo Putta:

Każda hierarchia techniczna z czasem rozwija inwersję kompetencji.

Stwierdzenia te sugerują, że ze względu na różne kryteria selekcji i trendy w organizacji grup, na szczeblach pracy organizacji technicznych znajdzie się pewna liczba wykwalifikowanych osób oraz pewna liczba osób na stanowiskach kierowniczych, które nie są świadome złożoności i wyzwań związanych z pracę, którą zarządzają. Może to być spowodowane zjawiskami takimi jak Zasada Petera lub Zasada Dilberta .

Należy jednak podkreślić, że takie przepisy są szerokimi uogólnieniami i mogą mieć zastosowanie do niektórych typów organizacji, a nie do innych.

Zobacz też:

Prawo Reeda

Prawo Reeda na Wikipedii

Użyteczność dużych sieci, w szczególności sieci społecznościowych, rośnie wykładniczo wraz z rozmiarem sieci.

Prawo to opiera się na teorii grafów, gdzie użyteczność skaluje się jako liczba możliwych podgrup, czyli szybciej niż liczba uczestników lub liczba możliwych połączeń parami. Odlyzko i inni argumentowali, że prawo Reeda zawyża użyteczność systemu, nie uwzględniając ograniczeń ludzkiego poznania w zakresie efektów sieciowych; zobacz Numer Dunbara .

Zobacz też:

Prawo zachowania złożoności (prawo Teslera)

Prawo zachowania złożoności na Wikipedii

Prawo to mówi, że w systemie występuje pewna złożoność, której nie można zredukować.

Pewna złożoność systemu jest „nieumyślna”. Jest to konsekwencja złej struktury, błędów lub po prostu złego zamodelowania problemu do rozwiązania. Przypadkową złożoność można zmniejszyć (lub wyeliminować). Jednak pewna złożoność jest „wewnętrzna” jako konsekwencja złożoności nieodłącznie związanej z rozwiązywanym problemem. Tę złożoność można przenieść, ale nie można jej wyeliminować.

Ciekawym elementem tego prawa jest sugestia, że nawet uproszczenie całego systemu nie zmniejsza wewnętrznej złożoności, lecz przenosi się na użytkownika , który musi zachowywać się w bardziej złożony sposób.

Prawo Demeter

Prawo Demeter na Wikipedii

Nie rozmawiaj z nieznajomymi.

Prawo Demeter, znane również jako „zasada najmniejszej wiedzy”, jest zasadą projektowania oprogramowania, szczególnie istotną w językach obiektowych.

Stwierdza, że jednostka oprogramowania powinna rozmawiać tylko ze swoimi bezpośrednimi współpracownikami. Obiekt A z odwołaniem do obiektu B może wywoływać swoje metody, ale jeśli B ma odwołanie do obiektu C , A nie powinien wywoływać C s. Tak więc, jeśli C ma doThing() , A nie powinien wywoływać jej bezpośrednio; B.getC().doThis() .

Przestrzeganie tej zasady ogranicza zakres zmian, czyniąc je łatwiejszymi i bezpieczniejszymi w przyszłości.

Prawo nieszczelnych abstrakcji

Prawo nieszczelnych abstrakcji dotyczących Joela na oprogramowaniu

Wszystkie nietrywialne abstrakcje są do pewnego stopnia nieszczelne.

( Joel Spolsky )

Prawo to stanowi, że abstrakcje, które są zwykle używane w obliczeniach w celu uproszczenia pracy ze skomplikowanymi systemami, w pewnych sytuacjach „wyciekają” elementy systemu bazowego, co powoduje, że abstrakcja zachowuje się w nieoczekiwany sposób.

Przykładem może być wczytanie pliku i odczytanie jego zawartości. Interfejsy API systemu plików są abstrakcją systemów jądra niższego poziomu, które same w sobie są abstrakcją fizycznych procesów związanych ze zmianą danych na talerzu magnetycznym (lub pamięci flash w przypadku dysku SSD). W większości przypadków zadziała abstrakcja traktowania pliku jako strumienia danych binarnych. Jednak w przypadku dysku magnetycznego sekwencyjny odczyt danych będzie znacznie szybszy niż dostęp losowy (ze względu na zwiększony narzut błędów stron), ale w przypadku dysku SSD ten narzut nie będzie obecny. Aby poradzić sobie z tym przypadkiem, należy zrozumieć podstawowe szczegóły (na przykład pliki indeksu bazy danych są skonstruowane tak, aby zmniejszyć obciążenie losowego dostępu), szczegóły implementacji „przecieków” abstrakcji, o których programista może być świadomy.

Powyższy przykład może stać się bardziej złożony, gdy zostanie wprowadzonych więcej abstrakcji. System operacyjny Linux umożliwia dostęp do plików przez sieć, ale reprezentowane lokalnie jako „normalne” pliki. Ta abstrakcja „przecieka” w przypadku awarii sieci. Jeśli programista traktuje te pliki jako „normalne” pliki, nie biorąc pod uwagę faktu, że mogą one podlegać opóźnieniom i awariom sieci, rozwiązania będą zawierały błędy.

Artykuł opisujący prawo sugeruje, że nadmierne poleganie na abstrakcjach w połączeniu ze słabym zrozumieniem procesów leżących u ich podstaw w rzeczywistości sprawia, że radzenie sobie z danym problemem w niektórych przypadkach staje się bardziej złożone.

Zobacz też:

Przykłady ze świata rzeczywistego:

Prawo trywialności

Prawo trywialności na Wikipedii

To prawo sugeruje, że grupy będą poświęcać znacznie więcej czasu i uwagi błahym lub kosmetycznym kwestiom niż poważnym i istotnym.

Powszechnie używanym fikcyjnym przykładem jest komitet zatwierdzający plany elektrowni jądrowej, który spędza większość czasu na omawianiu struktury szopy na rowery, a nie na znacznie ważniejszym projekcie samej elektrowni. Wniesienie wartościowego wkładu w dyskusje na bardzo duże, złożone tematy może być trudne bez wysokiego poziomu wiedzy merytorycznej lub przygotowania. Jednak ludzie chcą być postrzegani jako wnoszący cenny wkład. Stąd tendencja do skupiania zbyt dużej ilości czasu na drobnych szczegółach, które można łatwo wytłumaczyć, ale niekoniecznie mają one szczególne znaczenie.

Powyższy fikcyjny przykład doprowadził do użycia terminu „Zrzucanie rowerów” jako wyrażenia marnowania czasu na błahe szczegóły. Pokrewnym terminem jest „ golenie jaka”, które oznacza pozornie nieistotną czynność, która jest częścią długiego łańcucha warunków wstępnych do głównego zadania.

Filozofia Uniksa

Filozofia Uniksa na Wikipedii

Filozofia Uniksa polega na tym, że komponenty oprogramowania powinny być małe i skoncentrowane na robieniu jednej konkretnej rzeczy dobrze. Może to ułatwić budowanie systemów poprzez komponowanie małych, prostych, dobrze zdefiniowanych jednostek, zamiast używania dużych, złożonych, wielozadaniowych programów.

Nowoczesne praktyki, takie jak „architektura mikrousług”, można traktować jako zastosowanie tego prawa, w którym usługi są małe, skoncentrowane i wykonują jedną konkretną rzecz, umożliwiając złożone zachowanie złożone z prostych elementów konstrukcyjnych.

Zasada Skauta

Reguła Skauta na O’Reilly

Zawsze zostawiaj kod lepszy, niż go znalazłeś.

(Robert C. Martin (Wujek Bob))

Oparta na „Zasadze Zwiadowcy”, która mówi, że „zawsze zostawiaj pole kempingowe czystsze, niż go znalazłeś”, zasada zwiadu w programowaniu to po prostu „zawsze pozostawiaj kod czystszy, niż go znalazłeś”.

Zostało to wprowadzone w pierwszym rozdziale książki Czysty kod autorstwa Boba Martina. Reguła sugeruje, że programiści powinni przeprowadzać „optymistyczne refaktoryzację”, co oznacza dążenie do poprawy ogólnej jakości kodu podczas pracy nad nim. Jeśli zauważysz błąd, spróbuj go naprawić lub wyczyść. Jednak przy wprowadzaniu zmian w kodzie, który wydaje się niepoprawny, warto pamiętać o płocie Chestertona !

Zobacz też:

https://www.amazon.sg/Clean-Code-Handbook-Software-Craftsmanship/dp/0132350882

Model Spotify

Model Spotify w Spotify Labs

Model Spotify to podejście do struktury zespołu i organizacji spopularyzowane przez „Spotify”. W tym modelu zespoły są zorganizowane wokół funkcji, a nie technologii.

Model Spotify popularyzuje również koncepcje plemion, gildii, oddziałów, które są innymi elementami ich struktury organizacyjnej.

Członkowie organizacji opisali, że rzeczywiste znaczenie tych grup zmienia się, ewoluuje i jest ciągłym eksperymentem. Fakt, że model jest procesem w ruchu , a nie stałym modelem, nadal prowadzi do różnych interpretacji struktury, które mogą opierać się na prezentacjach wygłaszanych przez pracowników na konferencjach. Oznacza to, że „migawki” mogą być „przepakowywane” przez osoby trzecie w stałą strukturę , co powoduje utratę dynamiki modelu.

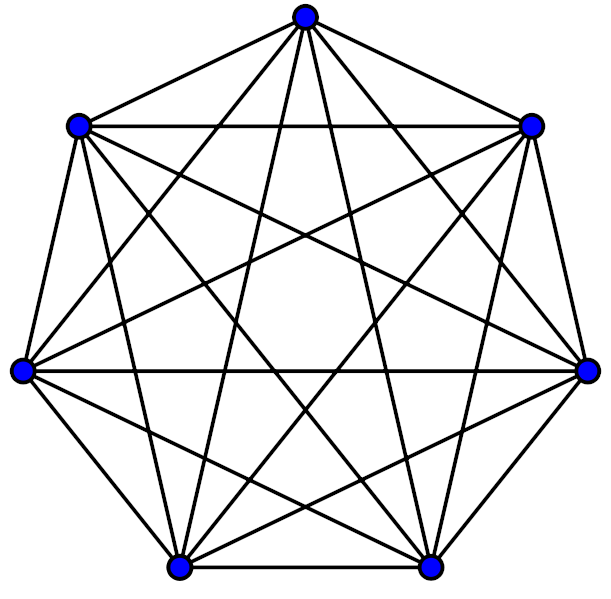
Zasada dwóch pizzy

Jeśli nie możesz nakarmić drużyny dwiema pizzami, jest za duża.

(Jeff Bezos)

Ta zasada sugeruje, że niezależnie od wielkości firmy, zespoły powinny być na tyle małe, aby mogły je nakarmić dwie pizze. Przekonanie to, przypisywane Jeffowi Bezosowi i Amazonowi, sugeruje, że duże zespoły są z natury nieefektywne. Potwierdza to fakt, że wraz ze wzrostem liczebności zespołu liniowo, powiązania między ludźmi rosną kwadratowo; w ten sposób koszt koordynacji i komunikacji również rośnie kwadratowo. Jeśli ten koszt koordynacji jest zasadniczo kosztowny, należy preferować mniejsze zespoły.

Liczbę powiązań między ludźmi można wyrazić jako n(n-1)/2 gdzie n = liczba osób.

Kompletny wykres; Powiązania między ludźmi

Prawo Wadlera

Prawo Wadlera na wiki.haskell.org

W każdym projekcie językowym całkowity czas poświęcony na omawianie funkcji z tej listy jest proporcjonalny do dwóch podniesionych do potęgi jej pozycji.

  1. Semantyka
  2. Składnia
  3. Składnia leksykalna
  4. Składnia leksykalna komentarzy

(W skrócie, na każdą godzinę spędzoną na semantyce, 8 godzin zostanie poświęconych na składnię komentarzy).

Podobnie jak Prawo trywialności, Prawo Wadlera mówi, że przy projektowaniu języka ilość czasu poświęcanego na struktury językowe jest nieproporcjonalnie duża w porównaniu z wagą tych cech.

Zobacz też:

Prawo Wheatona

Połączenie

Dzień Oficjalny

Nie bądź kutasem.

Wila Wheatona

Ukute przez Wila Wheatona (Star Trek: The Next Generation, The Big Bang Theory), to proste, zwięzłe i potężne prawo ma na celu zwiększenie harmonii i szacunku w profesjonalnej organizacji. Może być stosowany podczas rozmów ze współpracownikami, przeprowadzania przeglądów kodu, przeciwstawiania się innym punktom widzenia, krytykowania i ogólnie większości profesjonalnych interakcji między ludźmi.

Zasady

Zasady są zazwyczaj bardziej prawdopodobne jako wytyczne dotyczące projektowania.

Wszystkie modele są złe (prawo George’a Boxa)

Wszystkie modele są złe

Wszystkie modele są błędne, ale niektóre są przydatne.

George Box

Zasada ta sugeruje, że wszystkie modele systemów są wadliwe, ale dopóki nie są zbyt wadliwe, mogą być użyteczne. Zasada ta ma swoje korzenie w statystyce, ale odnosi się również do modeli naukowych i obliczeniowych.

Podstawowym wymaganiem większości oprogramowania jest modelowanie pewnego rodzaju systemu. Niezależnie od tego, czy modelowany system jest siecią komputerową, biblioteką, wykresem powiązań społecznościowych czy jakimkolwiek innym systemem, projektant będzie musiał określić odpowiedni poziom szczegółowości modelowania. Nadmierna szczegółowość może prowadzić do zbyt dużej złożoności, zbyt mała szczegółowość może uniemożliwić funkcjonowanie modelu.

Zobacz też:

Płot Chestertona

Płot Chestertona na Wikipedii

Nie należy przeprowadzać reform, dopóki nie zrozumie się uzasadnienia istniejącego stanu rzeczy.

Ta zasada jest istotna w inżynierii oprogramowania przy usuwaniu długu technicznego. Każda linia programu została z jakiegoś powodu napisana przez kogoś. Chesterton’s Fence sugeruje, że należy starać się w pełni zrozumieć kontekst i znaczenie kodu przed jego zmianą lub usunięciem, nawet jeśli na pierwszy rzut oka wydaje się on zbyteczny lub niepoprawny.

Nazwa tej zasady pochodzi od opowiadania GK Chestertona . Mężczyzna natrafia na płot przecinający środek drogi. Skarży się burmistrzowi, że to bezużyteczne ogrodzenie przeszkadza i prosi o jego usunięcie. Burmistrz pyta, dlaczego w ogóle jest tam ogrodzenie. Kiedy mężczyzna mówi, że nie wie, burmistrz mówi: „Jeśli nie znasz jego przeznaczenia, na pewno nie pozwolę ci go usunąć. to.”

Efekt Morza Martwego

Wpływ Morza Martwego na Bruce’a F. Webstera

„… [Z]iętniej utalentowani i skuteczni inżynierowie IT najczęściej odchodzą – by wyparować… [ci, którzy mają tendencję do pozostawania] w tyle [są] „pozostałościami” — najmniej utalentowanymi i skutecznymi inżynierami IT ”.

Bruce F. Webster

„Efekt Morza Martwego” sugeruje, że w każdej organizacji umiejętności/talent/skuteczność inżynierów są często odwrotnie proporcjonalne do ich czasu w firmie.

Zazwyczaj wysoko wykwalifikowani inżynierowie łatwo znajdują zatrudnienie gdzie indziej i są to pierwsi. Inżynierowie, którzy mają przestarzałe lub słabe umiejętności, zwykle pozostają w firmie, ponieważ znalezienie pracy w innym miejscu jest trudne. Jest to szczególnie widoczne, jeśli w ciągu swojego czasu w firmie uzyskali dodatkowe podwyżki płac, ponieważ uzyskanie ekwiwalentnego wynagrodzenia w innym miejscu może być trudne.

Zasada Dilberta

Zasada Dilberta na Wikipedii

Firmy mają tendencję do systematycznego awansowania niekompetentnych pracowników do kierownictwa, aby wydostać ich z przepływu pracy.

Scott Adams

Koncepcja zarządzania opracowana przez Scotta Adamsa (twórcę komiksu Dilberta), Zasada Dilberta jest inspirowana Zasadą Petera . Zgodnie z Zasadą Dilberta pracownicy, którzy nigdy nie byli kompetentni, są awansowani na stanowiska kierownicze w celu ograniczenia szkód, jakie mogą wyrządzić. Adams po raz pierwszy wyjaśnił tę zasadę w artykule Wall Street Journal z 1995 r., a następnie rozwinął ją w swojej książce biznesowej z 1996 r. „Zasada Dilberta” .

Zobacz też:

Zasada Pareto (Zasada 80/20)

Zasada Pareto na Wikipedii

Większość rzeczy w życiu nie jest rozłożona równomiernie.

Zasada Pareto sugeruje, że w niektórych przypadkach większość wyników pochodzi z mniejszości danych wejściowych:

W latach czterdziestych amerykańsko-rumuński inżynier dr Joseph Juran, powszechnie uważany za ojca kontroli jakości, zaczął stosować zasadę Pareto do kwestii jakości .

Ta zasada jest również znana jako: Reguła 80/20, Prawo Niewielu Witalnych oraz Zasada Rzadkości Czynników.

Przykłady ze świata rzeczywistego:

Zasada Shirky

Wyjaśnienie zasady Shirky

Instytucje będą starały się zachować problem, którego są rozwiązaniem.

Glina Shirky

Zasada Shirky sugeruje, że złożone rozwiązania – firma, branża lub technologia – mogą być tak skoncentrowane na problemie, który rozwiązują, że mogą nieumyślnie utrwalać sam problem. Może to być celowe (firma dążąca do znalezienia nowych niuansów problemu, które uzasadniają dalsze opracowywanie rozwiązania) lub nieumyślne (niezdolność lub niechęć do zaakceptowania lub zbudowania rozwiązania, które całkowicie rozwiąże problem lub go ominie).

Związany z:

Zobacz też:

Zasada Piotra

Zasada Piotra na Wikipedii

Ludzie w hierarchii mają tendencję do wznoszenia się do swojego „poziomu niekompetencji”.

Laurence J. Peter

Koncepcja zarządzania opracowana przez Laurence’a J. Petera, Zasada Petera, wskazuje, że ludzie, którzy są dobrzy w swojej pracy, są awansowani, dopóki nie osiągną poziomu, na którym nie odnoszą już sukcesów (ich „poziom niekompetencji”). W tym momencie, ponieważ są bardziej starsi, jest mniej prawdopodobne, że zostaną usunięci z organizacji (chyba że osiągają spektakularnie złe wyniki) i nadal będą pełnić rolę, w której mają niewiele wrodzonych umiejętności, ponieważ ich oryginalne umiejętności, które ich uczyniły sukces niekoniecznie są umiejętnościami wymaganymi w nowej pracy.

Jest to szczególnie interesujące dla inżynierów – którzy początkowo zaczynają od głęboko technicznych ról, ale często mają ścieżkę kariery, która prowadzi do zarządzania innymi inżynierami – co wymaga zasadniczo innego zestawu umiejętności.

Zobacz też:

Zasada solidności (prawo Postela)

Zasada solidności na Wikipedii

Bądź konserwatywny w tym, co robisz, bądź liberalny w tym, co akceptujesz od innych.

Zasada ta, często stosowana w tworzeniu aplikacji serwerowych, mówi, że to, co wysyłasz do innych, powinno być jak najmniejsze i zgodne, ale powinieneś dążyć do umożliwienia niezgodnych danych wejściowych, jeśli można je przetworzyć.

Celem tej zasady jest zbudowanie systemów, które są solidne, ponieważ mogą poradzić sobie ze źle sformułowanymi danymi wejściowymi, jeśli intencje mogą być nadal zrozumiałe. Jednak akceptowanie zniekształconych danych wejściowych może wiązać się z potencjalnymi implikacjami bezpieczeństwa, szczególnie jeśli przetwarzanie takich danych wejściowych nie jest dobrze przetestowane. Te implikacje i inne kwestie zostały opisane przez Erica Allmana w Reconsidered The Robustness Principle Reconsidered .

Dopuszczenie niezgodnych danych wejściowych z czasem może osłabić zdolność protokołów do ewolucji, ponieważ realizatorzy będą w końcu polegać na tej liberalności w budowaniu swoich funkcji.

Zobacz też:

SOLID

To jest akronim, który odnosi się do:

Są to kluczowe zasady programowania zorientowanego obiektowo . Zasady projektowania, takie jak te, powinny być w stanie pomóc programistom w tworzeniu systemów łatwiejszych w utrzymaniu.

Zasada pojedynczej odpowiedzialności

Zasada pojedynczej odpowiedzialności na Wikipedii

Każdy moduł lub klasa powinna mieć tylko jedną odpowiedzialność.

Pierwsza z zasad „ SOLID ”. Ta zasada sugeruje, że moduły lub klasy powinny robić jedną rzecz i tylko jedną rzecz. W bardziej praktycznym ujęciu oznacza to, że pojedyncza, niewielka zmiana w funkcji programu powinna wymagać zmiany tylko w jednym komponencie. Na przykład zmiana sposobu sprawdzania poprawności hasła pod kątem złożoności powinna wymagać zmiany tylko w jednej części programu.

Teoretycznie powinno to sprawić, że kod będzie bardziej niezawodny i łatwiejszy do zmiany. Wiedza, że zmieniany komponent ma tylko jedną odpowiedzialność, oznacza tylko, że testowanie tej zmiany powinno być łatwiejsze. Korzystając z wcześniejszego przykładu, zmiana składnika złożoności hasła powinna mieć wpływ tylko na funkcje związane ze złożonością hasła. O wiele trudniejsze może być uzasadnienie wpływu zmiany na element, który ma wiele obowiązków.

Zobacz też:

Zasada otwarcia/zamknięcia

Zasada otwarcia/zamknięcia na Wikipedii

Encje powinny być otwarte na rozszerzenie i zamknięte na modyfikację.

Druga z zasad „ SOLID ”. Zasada ta stwierdza, że encje (które mogą być klasami, modułami, funkcjami itd.) powinny mieć możliwość rozszerzenia ich zachowania, ale ich istniejące zachowanie nie powinno być modyfikowane.

Jako hipotetyczny przykład wyobraź sobie moduł, który jest w stanie zamienić dokument Markdown w HTML. Teraz wyobraź sobie, że do specyfikacji Markdown dodano nową składnię, która dodaje obsługę równań matematycznych. Moduł powinien być otwarty do rozbudowy w celu wdrożenia nowej składni matematycznej. Jednak istniejące implementacje składni (takie jak akapity, punktory itp.) powinny zostać zamknięte przed modyfikacją . Już działają, nie chcemy, żeby ludzie je zmieniali.

Ta zasada ma szczególne znaczenie w przypadku programowania obiektowego, w którym możemy projektować obiekty tak, aby można je było łatwo rozszerzać, ale unikamy projektowania obiektów, których istniejące zachowanie może zostać zmienione w nieoczekiwany sposób.

Zobacz też:

Zasada substytucji Liskov

Zasada substytucji Liskov na Wikipedii

Powinna istnieć możliwość zamiany typu na podtyp bez naruszania systemu.

Trzecia z zasad „ SOLID ”. Ta zasada mówi, że jeśli komponent opiera się na typie, powinien móc używać podtypów tego typu, bez awarii systemu lub konieczności poznania szczegółów tego podtypu.

Jako przykład wyobraźmy sobie, że mamy metodę, która odczytuje dokument XML ze struktury reprezentującej plik. Jeśli metoda używa typu podstawowego „plik”, to wszystko, co pochodzi od „plik”, powinno być możliwe do użycia w funkcji. Jeśli „plik” obsługuje wyszukiwanie wsteczne, a parser XML korzysta z tej funkcji, ale typ pochodny „plik sieciowy” nie powiedzie się podczas próby wyszukiwania wstecznego, wówczas „plik sieciowy” narusza tę zasadę.

Zasada ta ma szczególne znaczenie w przypadku programowania obiektowego, w którym hierarchie typów muszą być starannie modelowane, aby uniknąć dezorientacji użytkowników systemu.

Zobacz też:

Zasada segregacji interfejsów

Zasada segregacji interfejsów w Wikipedii

Żaden klient nie powinien być zmuszany do polegania na metodach, których nie używa.

Czwarta z zasad „ SOLID ”. Zasada ta stanowi, że konsumenci komponentu nie powinni zależeć od funkcji tego komponentu, z którego faktycznie nie korzysta.

Jako przykład wyobraźmy sobie, że mamy metodę, która odczytuje dokument XML ze struktury reprezentującej plik. Musi tylko czytać bajty, przesuwać się do przodu lub do tyłu w pliku. Jeśli ta metoda wymaga aktualizacji z powodu zmiany niepowiązanej cechy struktury pliku (takiej jak aktualizacja modelu uprawnień używanego do reprezentowania bezpieczeństwa plików), zasada została unieważniona. Byłoby lepiej, gdyby plik zaimplementował interfejs „przeszukiwanego strumienia” i aby czytnik XML go używał.

Zasada ta ma szczególne znaczenie dla programowania obiektowego, w którym interfejsy, hierarchie i typy abstrakcyjne są używane w celu zminimalizowania sprzężenia między różnymi komponentami. Wpisywanie kaczki to metodologia, która wymusza tę zasadę, eliminując jawne interfejsy.

Zobacz też:

Zasada odwrócenia zależności

Zasada odwrócenia zależności na Wikipedii

Moduły wysokopoziomowe nie powinny być zależne od implementacji niskopoziomowych.

Piąta z zasad „ SOLID ”. Ta zasada stanowi, że komponenty orkiestrujące wyższego poziomu nie powinny znać szczegółów ich zależności.

Jako przykład wyobraź sobie, że mamy program, który odczytuje metadane ze strony internetowej. Przyjęlibyśmy, że główny komponent musiałby wiedzieć o komponencie, aby pobrać zawartość strony internetowej, a następnie komponent, który może odczytać metadane. Gdybyśmy wzięli pod uwagę inwersję zależności, główny składnik zależałby tylko od abstrakcyjnego komponentu, który może pobierać dane bajtowe, a następnie od abstrakcyjnego komponentu, który byłby w stanie odczytać metadane ze strumienia bajtów. Główny komponent nie wiedziałby o TCP/IP, HTTP, HTML itp.

Ta zasada jest złożona, ponieważ może się wydawać, że „odwraca” oczekiwane zależności systemu (stąd nazwa). W praktyce oznacza to również, że oddzielny składnik orkiestracji musi zapewniać prawidłowe implementacje typów abstrakcyjnych (np. w poprzednim przykładzie coś musi nadal zapewniać składnik czytnika metadanych — narzędzie do pobierania plików HTTP i czytnik metatagów HTML). Następnie dotyka wzorców, takich jak Inversion of Control i Dependency Injection .

Zobacz też:

Zasada DRY

Zasada DRY na Wikipedii

Każda wiedza musi mieć jedną, jednoznaczną, autorytatywną reprezentację w ramach systemu.

DRY to akronim od Don’t Repeat Yourself . Ta zasada ma na celu pomóc programistom w zmniejszeniu powtarzalności kodu i utrzymaniu informacji w jednym miejscu i została przytoczona w 1999 roku przez Andrew Hunta i Dave’a Thomasa w książce The Pragmatic Developer

Przeciwieństwem DRY byłoby WET (Write Everything Twice lub We Enjoy Typing).

W praktyce, jeśli masz tę samą informację w dwóch (lub więcej) różnych miejscach, możesz użyć DRY, aby połączyć je w jedną i ponownie wykorzystać w dowolnym miejscu.

Zobacz też:

Zasada KISS

KISS na Wikipedii

Niech to będzie możliwie proste

Zasada KISS stwierdza, że większość systemów działa najlepiej, jeśli są proste, a nie skomplikowane; dlatego prostota powinna być kluczowym celem w projektowaniu i należy unikać niepotrzebnej złożoności. Pochodzące z US Navy w 1960 r. wyrażenie kojarzone jest z inżynierem lotniczym Kelly Johnson.

Zasadę tę najlepiej ilustruje historia Johnsona przekazującego zespołowi konstruktorów garść narzędzi, z wyzwaniem, że projektowany przez nich samolot odrzutowy musi być naprawiany przez przeciętnego mechanika w terenie w warunkach bojowych za pomocą tylko tych narzędzi. Stąd „głupia” odnosi się do związku między sposobem, w jaki rzeczy się psują, a wyrafinowaniem dostępnych narzędzi do ich naprawy, a nie możliwościami samych inżynierów.

Zobacz też:

YAGNI

YAGNI na Wikipedii

Jest skrótem dla Y Ou A in’t G onna N Id i t.

Zawsze wdrażaj rzeczy, kiedy naprawdę ich potrzebujesz, nigdy tylko wtedy, gdy tylko przewidujesz, że ich potrzebujesz.

( Ron Jeffries ) (współzałożyciel XP i autor książki „Zainstalowane programowanie ekstremalne”)

Ta zasada Extreme Programming (XP) sugeruje, że programiści powinni wdrażać tylko te funkcje, które są potrzebne do natychmiastowych wymagań i unikać prób przewidywania przyszłości poprzez implementację funkcji, które mogą być potrzebne później.

Przestrzeganie tej zasady powinno zmniejszyć ilość niewykorzystanego kodu w kodzie i uniknąć marnowania czasu i wysiłku na funkcjonalność, która nie przynosi żadnej wartości.

Zobacz też:

Błędy przetwarzania rozproszonego

Błędy przetwarzania rozproszonego na Wikipedii

Znane również jako Błędy Przetwarzania w Sieci , Błędy to lista przypuszczeń (lub przekonań) na temat przetwarzania rozproszonego, które mogą prowadzić do niepowodzeń w rozwoju oprogramowania. Założenia to:

Pierwsze cztery pozycje zostały wymienione przez Billa Joya i Toma Lyona około 1991 roku i po raz pierwszy sklasyfikowane przez Jamesa Goslinga jako „Fallacies of Networked Computing”. L. Peter Deutsch dodał błędy 5, 6 i 7. Pod koniec lat 90. Gosling dodał ósmy błąd.

Grupa została zainspirowana tym, co działo się w tym czasie w Sun Microsystems .

Te błędy powinny być uważnie brane pod uwagę podczas projektowania kodu, który jest odporny; zakładając, że którykolwiek z tych błędów może prowadzić do wadliwej logiki, która nie radzi sobie z rzeczywistością i złożonością systemów rozproszonych.

Zobacz też:

Lista rzeczy do przeczytania

Jeśli te koncepcje Cię zainteresowały, mogą Ci się spodobać następujące książki.

Zasoby online

Kilka przydatnych zasobów i lektur.

eBook w formacie PDF

Projekt jest dostępny jako eBook PDF, pobierz najnowszy eBook PDF za pomocą tego linku lub sprawdź stronę wydania starszych wersji.

Nowa wersja eBooka jest tworzona automatycznie po przekazaniu znacznika nowej wersji.

Podcast

Hacker Laws pojawił się w The Changelog , możesz sprawdzić odcinek podcastu, korzystając z poniższego linku:

Tłumaczenia

Dzięki wielu wspaniałym współpracownikom, Hacker Laws jest dostępny w wielu językach. Proszę rozważyć sponsorowanie moderatorów!

Język Moderator Status
🇮🇩 Bahasa Indonezja / indonezyjski arywidiantara
🇧🇷 Brasileiro/Brazylijski Eugênio Moreira , Leonardo Costa
🇨🇳 中文 / chiński Steve Xu Częściowo ukończony
🇩🇪 Niemiecki / Niemiecki Wiktor
🇫🇷 francuski / francuski Kevin Bockelandt
🇬🇷 ελληνικά / grecki Panagiotis Gourgaris
🇮🇹 Włoski/Włoski Claudio Sparpaglione Częściowo ukończony
🇯🇵 JP 日本語 / japoński Fumikazu Fujiwara
🇰🇷 한국어 / koreański Pączek Częściowo ukończony
🇱🇻 Latviešu Valoda / łotewski Artur Jansons
🇵🇱 Polski / Polish Mariusz Kogen
🇷🇺 Русская версия / rosyjski Alena Batitskaja Częściowo ukończony
🇪🇸 Castellano / hiszpański Manuel Rubio ( Sponsor ) Częściowo ukończony
🇹🇷 Turecki / Turecki Umut Işik
🇺🇦 українська мова / ukraiński Nazar , Helga Łastiwka

Jeśli chcesz zaktualizować tłumaczenie, postępuj zgodnie z Przewodnikiem dla współtwórców tłumaczy .

Powiązane projekty

Przyczynianie się

Prosimy o wkład! Zgłoś problem, jeśli chcesz zasugerować dodanie lub zmianę, lub Otwórz żądanie ściągnięcia, aby zaproponować własne zmiany.

Koniecznie przeczytaj Wytyczne dotyczące wkładu , aby poznać wymagania dotyczące tekstu, stylu i tak dalej. Prosimy o zapoznanie się z Kodeksem postępowania podczas dyskusji na temat projektu.

DO ZROBIENIA

Cześć! Jeśli wylądujesz tutaj, kliknąłeś link do tematu, którego jeszcze nie napisałem, przepraszam za to - prace w toku!

Możesz zgłosić problem, prosząc o więcej szczegółów lub otworzyć pull request, aby przesłać proponowaną definicję tematu.

This site is open source. Improve this page.