hacker-laws-website

💻📖 hacker-laws

Lois, théories, principes et modèles que les développeurs trouveront utiles.

Traductions: 🇧🇷 🇨🇳 🇩🇪 🇫🇷 🇬🇷 🇮🇹 🇱🇻 🇰🇷 🇷🇺 🇪🇸 🇹🇷

Vous aimez ce projet ? N’hésitez pas à me sponsoriser ainsi que les traducteurs.

Introduction
Lois
Principes
À lire
Traductions
Projets liés
Contribuer
TODO

Introduction

Il y a beaucoup de “lois” dont les gens parlent quand on discute de développement. Ce repository offre une vue d’ensemble et une référence des plus communes. N’hésitez pas à partager et à proposer vos PRs !

❗: Ce repo ne préconise aucune des lois, principes ou modèles qui y sont expliqués. Leur application devrait toujours être le sujet d’un débat, et dépend grandement de ce sur quoi vous travaillez.

Lois

Nous y voila !

Loi d’Amdahl

Loi d’Amdahl sur Wikipedia

La loi d’Amdahl est une formule qui montre le gain de vitesse potentiel sur un calcul, obtenu en augmentant les ressources d’un système. Habituellement utilisé en calcul parallèle, elle peut prédire les bénéfices réels de l’accroissement du nombre de processeurs. Bénéfices qui sont limités par le potentiel du programme à être parallélisé.

Prenons un exemple: si un programme est composé de 2 parties, la partie A devant être exécuté par un seul processeur et la partie B pouvant être parallélisée, alors on peut constater qu’ajouter plusieurs processeurs au système executant le programme ne peut avoir qu’un bénéfice limité. Cela peut potentiellement améliorer grandement la vitesse de la partie B, mais la vitesse de la partie A restera inchangée.

Le diagramme ci-dessous montre quelques exemples de gain de vitesse potentiels :

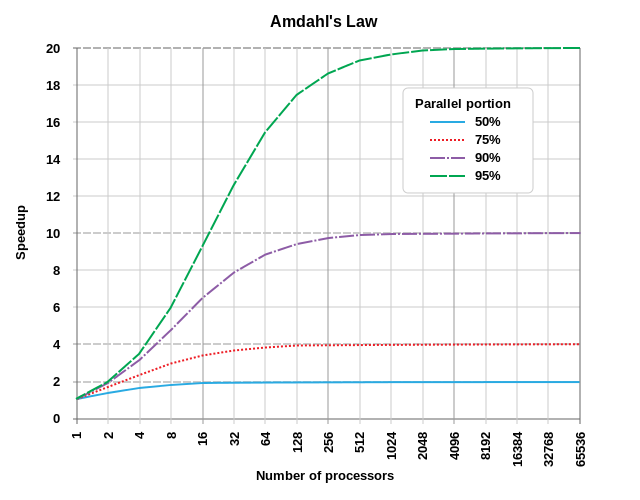
Diagram: Amdahl's Law

(Reference: par Daniels220 sur English Wikipedia, Creative Commons Attribution-Share Alike 3.0 Unported, https://en.wikipedia.org/wiki/File:AmdahlsLaw.svg)

Comme il est visible, un programme qui est parallélisable à 50% ne bénéficiera que très peu au delà des 10 processeurs, tandis qu’un programme parallélisable à 95% peut encore gagner en vitesse avec plus d’un millier de processeurs.

À mesure que la loi de Moore ralenti et que l’accélération de la vitesse de calcul des processeurs diminue, la parallélisation est la clef de l’amélioration des performances. Prenons par exemple la programmation graphique avec les calculs de Shader: chaque pixel ou fragment peut être rendu en parallèle. Ce qui explique que les cartes graphiques récentes ont souvent plusieurs milliers de coeurs de calcul (GPUs ou Shader Units).

Voir aussi:

Loi de Brooks
Loi de Moore

Théorie de la vitre brisée

Théorie de la vitre brisée sur Wikipedia

La théorie de la vitre brisée suggère que des signes visibles de criminalité (ou de manque de soin d’un environnement) amène à des crimes plus nombreux et plus sérieux (ou une plus grande détérioration de l’environnement).

Cette théorie est aussi appliqué au développement logiciel pour suggérer que du code de mauvaise qualité (ou de la dette technique) peut amener à penser que les efforts fait pour améliorer le code ne sont pas valorisés, voir complètement ignorés. Menant ainsi à une plus grande détérioration de la qualité du code au fil du temps.

Voir aussi:

Dette technique

Exemples:

Loi de Brooks

Loi de Brooks sur Wikipedia

Ajouter des personnes à un projet en retard accroît son retard.

Cette loi suggère que dans beaucoup de cas, tenter d’accélérer le bouclage d’un projet qui est en retard en ajoutant plus de personnes dessus rendra le projet encore plus en retard. Brooks est clair sur le fait qu’il s’agit d’une grande simplification, mais le raisonnement général est que la vitesse d’avancement du projet sur le court terme diminue à cause du temps nécessaire à l’intégration des nouveaux arrivants et du surplus de communication nécessaire. De plus, de nombreuses tâches peuvent ne pas être divisibles, comprendre réparties entre plusieurs personnes. Ce qui abaisse encore le potentiel d’augmentation de la vitesse d’avancement du projet.

La phrase bien connue “Neuf femmes ne peuvent pas faire un bébé en un mois” illustre la loi de Brooks, en particulier le fait que certaines tâches ne sont pas divisibles ou parallélisables.

C’est un thème central du livre ‘The Mythical Man Month’.

Voir aussi:

Death March
Reading List: The Mythical Man Month

Loi de Conway

Loi de Conway sur Wikipedia

Cette loi suggère que les contours techniques d’un système reflètent la structure de l’organisation qui a produit le système. Cette loi est souvent évoquée quand on cherche à améliorer l’organisation en question. Si une organisation est structurée en plusieurs unités déconnectées, le logiciel qui est produit le sera aussi. Si une organisation est composée de silos verticaux orientés autour de fonctionnalités ou services, le logiciel le reflètera aussi.

Voir aussi:

Modèle de Spotify

Loi de Cunningham

Loi de Cunningham sur Wikipedia

Le meilleur moyen d’obtenir une bonne réponse sur Internet n’est pas de poser la question, mais de poster la mauvaise réponse.

Selon Steven McGeady, Ward Cunningham lui aurait conseillé au début des années 1980: “le meilleur moyen d’obtenir une bonne réponse sur Internet n’est pas de poser la question, mais de poster la mauvaise réponse.” McGeady baptisa cette phrase la loi de Cunningham, bien que Cunningham lui même en réfute la parenté. Faisant initialement référence aux interactions sur Usenet, cette loi a été utilisé pour décrire le fonctionnement d’autres communautés en ligne (Wikipedia, Reddit, Twitter, Facebook).

Voir aussi:

XKCD 386: “Duty Calls”

Nombre de Dunbar

Nombre de Dunbar sur Wikipedia

“Le nombre de Dunbar est le nombre maximum d’individus avec lesquels une personne peut entretenir simultanément une relation humaine stable.” À savoir une relation dans laquelle un individu sait qui est chaque personne et comment elle est liée aux autres personnes. Il n’y a pas de véritable consensus sur le nombre exact. “… [Dunbar] avance que les êtres humains peuvent maintenir confortablement seulement 150 relations stables”. Il place le nombre dans un contexte social: “le nombre de personnes envers lesquelles vous ne vous sentiriez pas embarrassé de partager un verre si vous les croisiez par hasard dans un bar”. Les estimations du nombre tombent généralement entre 100 et 250.

De même que les relations stables entre individus, la relation entre un développeur et une codebase requiert des efforts pour être maintenu. Lorsque nous faisons face à de larges projets compliqués ou nombreux, nous pouvons nous aider de conventions, de procédures ou de modèles. Le nombre de Dunbar est important à garder à l’esprit non seulement lorsque la taille d’une entreprise augmente mais aussi lorsqu’on décide de la portée des efforts à réaliser pour une équipe. Pris dans un contexte d’ingénierie, il représente le nombre de projets sur lesquels on pourrait sereinement faire du support si on y était amené.

Voir aussi :

Loi de Conway

Loi de Gall

Loi de Gall sur Wikipedia

Un système complexe qui fonctionne est une évolution d’un système simple qui fonctionne. Un système complexe entièrement conçu depuis zero ne fonctionne jamais et ne peut pas être modifié pour le faire fonctionner. Il faut recommencer avec un système simple qui fonctionne. (John Gall)

La loi de Gall implique que les tentatives de concevoir un système fortement complexe ont de grandes chances d’échouer. Les systèmes fortement complexes sont rarement construits d’un seul coup, mais évoluent plutôt depuis des systèmes plus simples.

Un exemple classique est le world-wide-web. Dans son état actuel, il s’agit d’un système fortement complexe. Cependant, il était initialement définit comme un simple moyen d’échanger du contenu entre établissements universitaires. Ayant atteint cet objectif avec un grand succès, le système a évolué pour devenir de plus en plus complexe au fil du temps.

Voir aussi :

KISS (Keep It Simple, Stupid)

Loi de Goodhart

Loi de Goodhart sur Wikipedia

Toute régularité statistique observée a tendance à perdre de sa fiabilité lorsque on tente de la contrôler. Charles Goodhart

Souvent aussi énoncée de cette manière :

Lorsqu’une mesure devient un objectif, elle cesse d’être une bonne mesure. Marilyn Strathern

Cette loi indique que les optimisations basées sur une mesure peuvent amener à une perte de valeur de la mesure elle même. Un ensemble de mesures (KPIs) trop restraint appliqué aveuglément à un process déforme le résultat. Les gens tendent à “tricher” localement pour satisfaire une mesure en particulier sans faire attention aux effets globaux de leurs actions sur le système.

Exemples concrets :

Il est possible d’atteindre un taux de couverture du code arbitraire en rédigeant des tests qui ne vérifient rien. Alors que le but initial de la mesure était d’avoir du code correctement testé.
Mesurer les performances des développeurs avec le nombre de lignes de code rédigées amène à des codebases inutilement grosses.

Voir aussi :

Rasoir de Hanlon

Rasoir de Hanlon sur Wikipedia

Ne jamais attribuer à la malveillance ce que la bêtise suffit à expliquer. Robert J. Hanlon

Ce principe suggère que des actions produisant un mauvais résultat ne sont pas toujours motivées par de mauvaises intentions. Il est au contraire plus probable que le problème se situe dans la compréhension de ces actions et de leurs impacts.

Loi de Hofstadter

Loi de Hofstadter sur Wikipedia

Il faut toujours plus de temps que prévu, même en tenant compte de la loi de Hofstadter. (Douglas Hofstadter)

Vous pourrez entendre parler de cette loi lorsqu’on cherche à estimer le temps nécessaire pour faire quelque chose. C’est un lieu commun de dire que nous ne sommes pas très bon pour estimer le temps nécessaire à boucler un projet en développement logiciel.

c’est un extrait du livre ‘Gödel, Escher, Bach: An Eternal Golden Braid’.

Voir aussi :

À lire: Gödel, Escher, Bach: An Eternal Golden Braid

Loi de Hutber

Loi de Hutber sur Wikipedia

Amélioration veut dire détérioration. (Patrick Hutber)

Cette loi suggère que les améliorations apportées à un système vont mener à la détérioration d’autres choses. Ou qu’elles vont cacher d’autres détériorations, amenant globalement à une dégradation de l’état du système.

Par exemple, un abaissement de la latence de réponse sur une route (end-point) peut causer des problèmes de débit et de capacité plus loin, affectant un sous-système entièrement différent.

Cycle du hype & Loi d’Amara

Cycle du hype sur Wikipedia

On a tendance à surestimer l’effet d’une technologie sur le court terme et à le sous-estimer sur le long terme. (Roy Amara)

Le cycle du hype est une représentation visuelle de l’attrait et du développement d’une technologie au fil du temps. Initialement réalisé par Gartner, le concept est plus clair avec un diagramme :

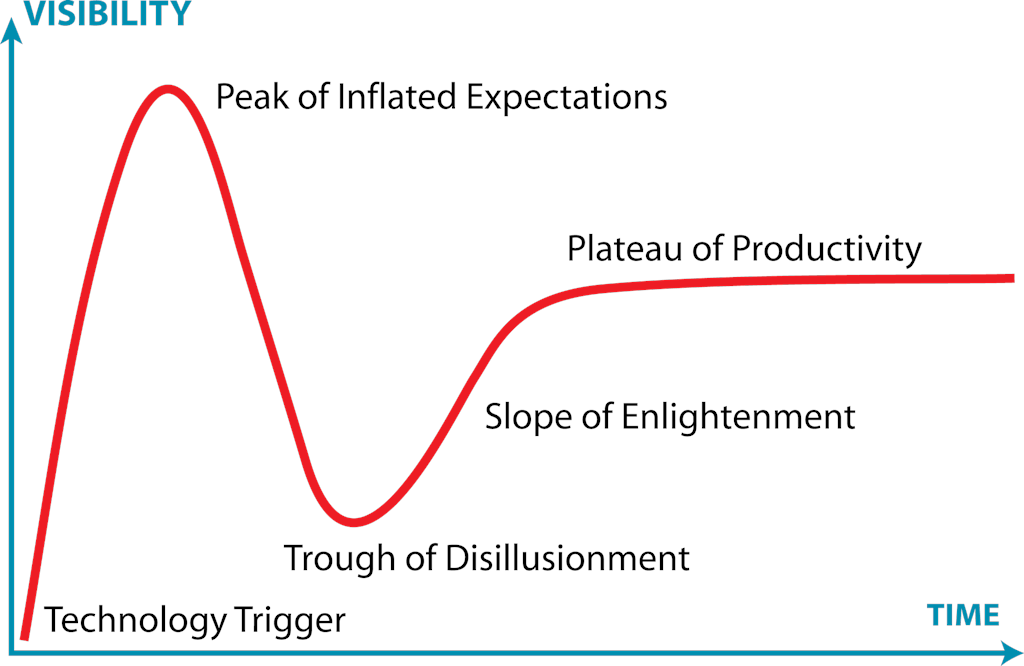
The Hype Cycle

(Reference: par Jeremykemp sur English Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10547051)

En clair, ce cycle montre qu’il y a généralement un pic d’excitation concernant les nouvelles technologies et leur potentiel impact. Les équipes adoptent ces technologies rapidement et se retrouvent parfois déçues des résultats. Cela peut être à cause d’un manque de maturité de la technologie, ou parce que les applications concrètes de cette technologie ne sont pas encore totalement maitrisées. Après un certain temps, les opportunités d’utiliser cette technologie ainsi que ses capacités augmentent suffisamment pour que les équipes deviennent vraiment productives. La citation de Roy Amara le résume de manière plus succincte: “On a tendance à surestimer l’effet d’une technologie sur le court terme et à le surestimer sur le long terme”.

Loi d’Hyrum (loi des interfaces implicites)

Loi d’Hyrum en ligne

Passé un certain nombre d’utilisateur d’une API, peu importe ce qui est promis par l’interface, tous les comportements possibles du système seront utilisés. (Hyrum Wright)

La loi d’Hyrum décris le fait que lorsqu’une API a un nombre suffisamment élevé d’utilisateurs, tous les comportements de l’API (y compris ceux qui ne sont pas définis publiquement) seront utilisés par quelqu’un. Un exemple trivial peut concerner les éléments non fonctionnels de l’API comme le temps de réponse. Un exemple plus subtil peut être l’utilisation d’une regex sur les messages d’erreurs pour en déterminer le type. Même si la spécification de l’API ne mentionne rien quant au contenu des messages, certains utilisateurs peuvent utiliser ces messages. Un changement au niveau de ces messages reviendrait à casser l’API pour ces utilisateurs.

Voir aussi :

Loi des abstractions qui fuient
XKCD 1172

Loi de Kernighan

Debugger est deux fois plus difficile que de rédiger le code initial. Par conséquent si vous rédiger le code de manière aussi maligne que possible, vous n’êtes, par définition, pas assez intelligent pour le debugger. (Brian Kernighan)

La loi de Kernighan est nommée d’après Brian Kernighan et est basée d’une citation du livre de Kernighan et Plauger: The Elements of Programming Style.

Tout le monde sait que debugger est 2 fois plus difficile que de rédiger le programme en premier lieu. Donc si vous êtes aussi malin que possible en le rédigeant, comment pourrez vous le debugger ?

Bien qu’étant hyperbolique, la loi de Kernighan présente l’argument que du code simple est préférable à du code complexe, car tout problème qui pourrait apparaitre dans du code complexe sera couteux voir impossible à debugger.

Voir aussi :

Principe KISS
Philosophie d’Unix
Rasoir d’Occam

Loi de Metcalfe

Loi de Metcalfe sur Wikipedia

L’utilité d’un réseau est proportionnelle au carré du nombre de ses utilisateurs.

Cette loi est basée sur le nombre de connexions par pair à l’intérieur d’un système et est fortement liée à la Loi de Reed. Odlyzko et d’autres ont soutenus l’argument que la loi de Reed et la loi de Metcalfe surestiment la valeur du système en ne tenant pas compte des limites de l’intellect humain. Voir le Nombre de Dunbar.

Voir aussi :

Loi de Reed
Nombre de Dunbar

Loi de Moore

Loi de Moore sur Wikipedia

Le nombre de transistors dans un circuit intégré double approximativement tous les 2 ans.

Souvent utilisée pour illustrer la grande vitesse à laquelle les semi-conducteurs et les technologies de puces informatiques ont évoluées. Cette prédiction de Moore s’est révélée être très précise des années 70 aux années 2000. Plus récemment ceci dit, la tendance a ralentie, en partie du aux limites physiques de la miniaturisation des composants. Cependant, les avancées dans la parallélisation et les changements potentiellement révolutionnaires dans les technologies des semi-conducteurs et du calcul quantique continueront peut être de faire respecter la loi de Moore pour les décennies à venir.

Loi de Murphy / Loi de Sod

Loi de Murphy sur Wikipedia

Tout ce qui est susceptible d’aller mal, ira mal.

Énoncée par Edward A. Murphy, Jr, la loi de Murphy déclare que si quelque chose peut mal tourner, cela tournera mal.

C’est une formule bien connue des développeurs. Parfois l’inattendu surviens lors du développement, des tests, ou même en production. Cette loi peut aussi être liée à la loi de Sod (plus courante en Anglais d’Angleterre) :

Si quelque chose peut mal tourner, cela tournera mal. Au pire moment possible.

Ces ‘lois’ sont souvent utilisées dans un sens humoristique. Cependant, des biais cognitifs tels que le biais de confirmation et le biais de sélection peuvent amener des gens à porter trop d’importance à ces lois. (On ne porte pas attention aux choses quand elles fonctionnent, la plupart du temps. Quand il y a un problème en revanche, c’est plus remarqué et peut entrainer des discussions)

Voir aussi :

Biais de confirmation
Biais de sélection

Rasoir d’Occam

Rasoir d’Occam sur Wikipedia

Les multiples ne doivent pas être utilisés sans nécessité. William of Ockham

Le rasoir d’Occam nous indique que parmi plusieurs solutions possibles, la plus probable est celle à laquelle est attachée le moins de concepts et d’à priori. Cette solution est la plus simple et résout le problème donné sans ajouter accidentellement de la complexité et de potentielles conséquences négatives.

Voir aussi :

Exemple :

Lean Software Development: Eliminate Waste

Loi de Parkinson

Loi de Parkinson sur Wikipedia

Le travail s’étale de façon à occuper le temps disponible pour son achèvement.

Dans son contexte original, cette loi était basée sur l’étude des administrations. Elle peut être appliquée aux projets de développement logiciel, la théorie étant que les équipes seront inefficaces jusqu’à l’approche des deadlines puis se dépêcheront de finir le travail pour tenir les délais. Rendant la deadline plus ou moins arbitraire.

Si cette loi est combinée avec la loi de Hofstadter, on arrive à une perspective encore plus pessimiste: le travail s’étale pour occuper tout le temps disponible et au final prendra encore plus de temps que prévu.

Voir aussi :

Loi de Hofstadter

Effet d’optimisation prématurée

Optimisation prématurée sur WikiWikiWeb

L’optimisation prématurée est la source de tous les maux. (Donald Knuth)

Dans l’article Structured Programming With Go To Statements rédigé par Donald Knuth, celui-ci écrit : “Les programmeurs perdent un temps énorme à réfléchir ou à se soucier de la vitesse de certaines parties non-critiques de leurs programmes. Et ces tentatives d’être performant ont en vérité un impact fortement négatif quand on prend en compte le debugging et la maintenance. Nous devrions oublier les petits rendements. Disons que 97% du temps: l’optimisation prématurée est la source de tous les maux. Ceci dit, nous ne devrions pas louper les opportunités disponibles dans ces 3% cruciaux.”

L’optimisation prématurée peut aussi être définie plus simplement comme: optimiser avant qu’on soit sûr qu’il faille le faire.

Loi de Putt

Loi de Putt sur Wikipedia

La technologie est dominée par deux types de personnes: celles qui comprennent ce qu’elles ne managent pas et celles qui managent ce qu’elles ne comprennent pas.

La loi de Putt est souvent suivie par sa corollaire :

Toute hiérarchie technique développe tôt ou tard une inversion de compétence.

Ces déclarations suggèrent que étant donné les divers critères de sélection et tendances dans la manière dont les groupes s’organisent, on trouvera au sein d’une entreprise technique deux types d’employés: des employés compétents techniquement non cadres et des employés à des postes de gestion qui ne comprennent pas aussi bien la complexité et les difficultés techniques. Cela peut être attribué à des phénomènes comme le principe de Peter or le principe de Dilbert.

Ceci dit, il est important de préciser que ce genre de lois sont des généralisations et s’appliquent à certains types d’organisation, sans s’appliquer à d’autres.

Voir aussi :

Principe de Peter
Principe de Dilbert

Loi de Reed

Loi de Reed sur Wikipedia

L’utilité des grands réseaux, particulièrement des réseaux sociaux, s’accroit exponentiellement avec la taille du réseau.

Cette loi est basée sur la théorie des graphs, où l’utilité s’accroit avec le nombre de sous-groupes possibles. Odlyzko et d’autres ont avancé l’argument que la loi de Reed surestime l’utilité du réseau en ne prenant pas en compte les limites du cerveau humain; voir le nombre de Dunbar.

Voir aussi :

Loi de Metcalfe
Nombre de Dunbar

Loi de la conservation de la complexité (Loi de Tesler)

Loi de la conservation de la complexité sur Wikipedia

Cette loi énonce qu’il y a une certaine quantité de complexité dans un système qui ne peut pas être réduite.

Une partie de la complexité d’un système est du à de la négligence. Conséquence d’une mauvaise structure, d’erreurs ou d’une mauvaise modélisation du problème à résoudre. Ce type de complexité peut être réduit, voir éliminé. Cependant, il y a une autre partie de la complexité qui est intrinsèque, du au problème qu’on cherche à résoudre. Ce type de complexité peut être déplacé mais pas éliminé.

Un élément interessant soulevé par cette loi est la suggestion que même en simplifiant le système en entier, la complexité intrinsèque n’est pas réduite, elle est déportée sur l’utilisateur, qui doit alors compenser.

Loi des abstractions qui fuient

Loi des abstractions qui fuient sur Joel on Software

Toutes les abstractions non-triviales fuient plus ou moins. (Joel Spolsky)

Cette loi énonce que les abstractions, qui sont généralement utilisé en informatique pour simplifier l’utilisation de systèmes complexes, vont “fuirent” une partie du système sous-jacent dans certaines situations.

Si on prends l’exemple de la lecture d’un fichier. Les APIs pour les systèmes de fichier sont une abstraction des systèmes plus bas niveau du kernel, qui sont eux même une abstraction du processus physique de changement de données sur le disque (ou la mémoire flash pour un SSD). Dans la plupart des cas, l’abstraction consistant à traiter un fichier comme un flux de données binaire fonctionnera comme prévu. Cependant, avec un disque magnétique la lecture de données séquentielle sera significativement plus rapide que la lecture de données aléatoire (due aux couts plus élevés d’erreurs de page). Mais pour un disque SSD, ces couts supplémentaires n’existent pas. On peut donc voir que les détails sous-jacents doivent être compris pour gérer cet exemple efficacement (par exemple les fichiers d’index de base de données sont structurés de manière à limiter le surcout des accès aléatoires). L’abstraction “fuit” certains détails d’implémentation que le développeur peut donc avoir besoin de connaitre.

L’exemple ci-dessus peut devenir plus complexe quand des abstractions supplémentaires sont présentes. Par exemple, le système d’exploitation Linux permet aux fichiers d’accéder à des fichiers via un réseau, mais les présente sur la machine comme étant “normaux”. Cette abstraction va fuir s’il y a des problèmes de réseau. Si un développeur traite ces fichiers comme étant “normaux” sans considérer le fait qu’ils peuvent être sujets à de la latence ou des échecs réseaux, le logiciel fonctionnera mal.

L’article décrivant cette loi suggère qu’une dépendance trop forte aux abstractions combinée à une faible compréhension des processus sous-jacent rend le problème plus complexe à gérer dans certains cas.

Voir aussi :

Loi d’Hyrum

Exemples concrets :

- Démarrage lent de Photoshop - un problème que j’ai eut par le passé. Photoshop était lent au démarrage, prenant parfois plusieurs minutes. Le problème venait du fait que le logiciel récupérait des informations sur l’imprimante par défaut au démarrage. Hors, si cette imprimante était reliée par réseau, cela prenait extrêmement longtemps. L’abstraction de l’imprimante réseau présentée comme étant similaire à une imprimante locale causait ce problème pour les utilisateurs avec une mauvaise connexion.

Loi de futilité

Loi de futilité sur Wikipedia

Cette loi suggère que les organisations donnent largement plus de temps et d’attention à des détails triviaux ou cosmétiques qu’aux problèmes fondamentaux et difficiles.

L’exemple fictif couramment utilisé est celui d’un comité approuvant les plans d’une centrale nucléaire et qui passe la majorité de son temps à parler du local à vélo plutôt que de la conception de la centrale en elle même. Il peut être difficile de participer de manière utile à des discussions concernant des sujets vastes et complexes sans une grande expertise ou préparation. Cependant les gens veulent être vu comme participant de manière utile. D’où une tendance à trop se focaliser sur des détails qui peuvent être abordés simplement mais qui n’ont pas particulièrement d’importance.

L’exemple ci-dessus à conduit à l’utilisation du terme ‘Bike Shedding’ (en rapport à l’abri à vélo) comme expression désignant une perte de temps sur des détails triviaux. Un autre terme apparenté est ‘Yak Shaving’, qui désigne une activité apparemment inutile qui fait partie d’une longe chaine de pré-requis à la tâche principale.

Philosophie d’Unix

The Unix Philosophie d’Unix sur Wikipedia

La philosophie d’Unix consiste à dire que les programmes informatiques doivent être petits, ne faire qu’une seule chose et la faire bien. Cela peut rendre plus simple la construction de systèmes en combinant des unités simples petites et bien définies plutôt que des programmes larges, complexes et servant à plusieurs choses.

Certaines pratiques récentes comme l’architecture en microservices peut être vue comme une application de cette loi, où les services sont petits et ne font qu’une seule chose, permettant la création de comportements complexes à partir de briques qui sont simples.

Modèle de Spotify

Modèle de Spotify sur Spotify Labs

Le modèle de Spotify est une approche à la structure d’entreprise et des équipes qui a été popularisée par Spotify. Dans ce modèle, les équipes sont organisées autour des fonctionnalités plutôt que des technologies.

Le modèle de Spotify a également popularisé les concepts de Tribus, Guildes, et Chapitres qui sont d’autres éléments de leur structure.

Loi de Wadler

Loi de Wadler sur wiki.haskell.org

Dans toute conception de langage, le temps total passé à discuter un aspect de cette liste est proportionnel à deux élevé à la puissance de la position correspondante.

Sémantique

Syntaxe

Syntaxe lexicale

Syntaxe lexicale des commentaires (en clair, pour chaque heure passée sur la sémantique, 8 heures seront passées sur la syntaxe des commentaires)

Similaire à la loi de trivialité, la loi de Wadler énonce que lors de la conception d’un langage, le temps passé à discuter des différents aspects est inversement proportionnel à l’importance de ces aspects.

Voir aussi :

Loi de futilité

Loi de Wheaton

Le lien

Le jour officiel

Ne soyez pas un connard. Wil Wheaton

Inventée par Will Wheaton (Star Trek: The Next Generation, The Big Bang Theory), cette loi simple, concise et puissante vise à augmenter l’harmonie et le respect au sein d’un environnement professionnel. Elle peut être appliquée lorsqu’on parle à ses collègues, effectue une revue de code (code review), argumente contre un autre point de vue, critique et de manière générale, lors de la plupart des interactions entre humains.

Principes

Les principes sont généralement des lignes directrices liés à la conception.

Principe de Dilbert

Principe de Dilbert sur Wikipedia

Les entreprises tendent à promouvoir systématiquement les employés incompétents afin de les sortir du workflow. Scott Adams

Un concept de gestion inventé par Scott Adams (créateur du comic strip Dilbert) inspiré par le principe de Peter. Suivant le principe de Dilbert, les employés qui n’ont jamais montré de compétence dans leur travail sont promus à des postes de management afin de limiter les dommages qu’ils peuvent causer. Adams expliqua initialement le principe dans un article du Wall Street Journal datant de 1995, et élabora le concept dans son livre de 1996: The Dilbert Principle.

Voir aussi :

Principe de Peter
Loi de Putt

Principe de Pareto (règle des 80/20)

Principe de Pareto sur Wikipedia

La plupart des choses dans la vie ne sont pas réparties également.

Le principe de Pareto suggère que dans certains cas, la majorité des résultats provient d’une minorité des actions :

80% d’un certain logiciel peut être écrit en 20% du temps de développement alloué (inversement, les 20% les plus difficiles prennent 80% du temps)
20% de l’effort fourni produit 80% du résultat
20% du travail amène 80% des revenus
20% des bugs causent 80% des crashs
20% des fonctionnalités entrainent 80% de l’utilisation

Dans les années 1940, l’ingénieur Américano-Roumain Dr. Joseph Juran, qui est largement crédité comme étant le père du contrôle qualité, commença à appliquer le principe de Pareto pour résoudre des problèmes de qualité.

Ce principe est aussi connu comme la règle des 80/20, ‘The Law of the Vital Few’ et ‘The Principle of Factor Sparsity’.

Exemples concrets :

- En 2002, Microsoft reporta qu’en réglant les 20% des bugs les plus reportés, 80% des erreurs et des crashs liés dans Windows et Office ont été éliminés (Reference).

Principe de Peter

Principe de Peter sur Wikipedia

Les gens faisant partie d’une hiérarchie tendent à s’élever à leur “niveau d’incompétence” Laurence J. Peter

Le principe de Peter est un concept de management inventé par Laurence J. Peter qui observe que les gens qui sont bons dans leur travail sont promus jusqu’à ce qu’ils atteignent un niveau où ils ne réussissent plus (leur “niveau d’incompétence”). À ce point, étant donné leur expérience ils sont moins susceptibles de se faire renvoyer (à part s’ils obtiennent des résultats particulièrement mauvais) et vont demeurer dans un poste pour lequel ils ont potentiellement peu de compétences.

Ce principe est particulièrement intéressant pour les ingénieurs qui démarrent leur carrière dans des postes profondément techniques mais évoluent souvent vers des postes de managers, qui requiert des compétences fondamentalement différentes.

Voir aussi :

Principe de Dilbert
Loi de Putt

Principe de robustesse (loi de Postel)

Principe de robustesse sur Wikipedia

Soyez tolérant dans ce que vous acceptez, et pointilleux dans ce que vous envoyez

Souvent appliqué dans le développement d’application serveur, ce principe énonce que ce que vous envoyez aux autres devrait être aussi minimal et conforme que possible. Mais que vous devriez accepter des données en entrée non-conforme si elles peuvent être traités.

Le but de ce principe est de construire des systèmes qui sont robustes dans le sens où ils peuvent gérer des entrées mal formées du moment qu’elles restent compréhensibles. Cependant, il y a de potentielles implications de sécurité à accepter des entrés mal formées. Particulièrement si le traitement de ces entrées n’est pas correctement testé.

À terme, autoriser des entrées non-conforme peut amoindrir la capacité d’évolution des protocoles étant donné que les utilisateurs vont tôt ou tard compter sur cette tolérance lors de leur utilisation.

Voir aussi :

Loi d’Hyrum

SOLID

Il s’agit d’un acronyme qui signifie :

S: Single responsibility principle (principe de responsabilité unique)
O: The Open/Closed Principle (principe ouvert/fermé)
L: The Liskov Substitution Principle (Principe de substitution de Liskov)
I: The Interface Segregation Principle (principe de ségrégation des interfaces)
D: Principe d’inversion des dépendances

Ces principes sont fondamentaux dans la programmation orientée objet. Ces principes de conception devraient pouvoir aider les développeurs à construire des systèmes plus facilement maintenable.

Principe de responsabilité unique

Principe de responsabilité unique sur Wikipedia

Chaque module ou classe ne doit avoir qu’une seule responsabilité.

Le premier des principes ‘SOLID’. Il suggère que les modules ou classes ne devraient faire qu’une chose unique. Autrement dit, un seul petit changement sur une fonctionnalité d’un programme ne devrait nécessiter de changer qu’un seul composant. Par exemple, changer la manière de valider un mot de passe ne devrait nécessiter un changement qu’à un endroit du programme.

Théoriquement, cela devrait rendre le code plus robuste et plus simple à modifier. Savoir qu’un composant en train d’être modifié possède une seule responsabilité veut aussi dire que tester cette modification devrait être plus simple. Pour reprendre l’exemple precedent, changer le composant concernant la validation d’un mot de passe ne devrait affecter que cette fonctionnalité. Il est souvent beaucoup plus difficile de réfléchir aux impacts d’un changement sur un composant qui est responsable de plusieurs choses.

Voir aussi :

Programmation orientée objet
SOLID

Principe ouvert/fermé

Principe ouvert/fermé sur Wikipedia

Les entités devraient être ouvertes à l’extension et fermées à la modification.

Le deuxième des principes ‘SOLID’. Il énonce que le comportement des entités (classes, modules, fonctions, etc.) devrait être étendu, mais que le comportement existant ne devrait pas être modifié.

Imaginons par exemple un module capable de changer un document rédigé en Markdown en HTML. Ce module peut être étendu en y ajoutant le support pour une nouvelle fonctionnalité Markdown sans modifier son fonctionnement interne. Le module est en revanche fermé à la modification dans le sens où un utilisateur ne peut pas changer la manière dont le code existant est rédigé.

Ce principe est particulièrement pertinent pour la programmation orientée objet, où on cherche la plupart du temps à concevoir des objets qu’on puisse facilement étendre mais dont le comportement existant ne puisse pas être modifié de manière imprévue.

Voir aussi :

Programmation orientée objet
SOLID

Principe de substitution de Liskov

Principe de substitution de Liskov sur Wikipedia

Il devrait être possible de remplacer un type avec un sous-type sans casser le système.

Le troisième des principes ‘SOLID’. Il énonce que si un composant repose sur un type, alors il devrait être capable d’utiliser un sous-type de ce type sans que le système ne plante ou qu’il y ai besoin de connaitre les détails de ce sous-type.

Imaginons par exemple que nous ayons une méthode qui lit un document XML depuis une structure représentant un fichier. Si cette méthode utilise un type ‘fichier’ de base, alors tous les types dérivant de ‘fichier’ devraient pouvoir être utilisé avec cette fonction. Si ‘fichier’ supporte une recherche partant de la fin et que le parser XML utilise cette fonction, mais que le type dérivé ‘fichier réseau’ ne permet pas de recherche en partant de la fin, alors ‘fichier réseau’ viole le principe.

Ce principe est particulièrement pertinent pour la programmation orientée objet, où les hierarchies de types doivent être conçues soigneusement pour éviter de brouiller les utilisateurs d’un système.

Voir aussi :

Programmation orientée objet
SOLID

Principe de ségrégation des interfaces

Principe de ségrégation des interfaces sur Wikipedia

Aucun client de devrait dépendre de méthodes qu’il n’utilise pas.

Le quatrième des principes ‘SOLID’. Celui-ci énonce que les utilisateurs d’un composant ne devraient pas dépendre des fonctions de ce composant qu’il n’utilise pas.

Par exemple, imaginons que nous ayons une méthode qui lit un document XML depuis une structure représentant un fichier. Elle nécéssite seulement de pouvoir lire des octets, avancer ou reculer dans le fichier. Le principe sera invalidé si cette méthode a besoin d’être mise à jour lorsqu’une fonctionnalité sans rapport du fichier change (ex. une mise à jour de modèle de permissions pour l’accès au fichier). Il serait préférable pour le fichier d’implémenter une interface ‘seekable-stream’, et pour le lecteur XML de l’utiliser.

Ce principe est particulièrement pertinent pour la programmation orientée objet, où les interfaces, hierarchies et type abstraits sont utilisés pour minimiser le couplage entre les différents composants. Le duck typing est une méthode qui applique ce principe en éliminant les interfaces explicites.

Voir aussi :

Programmation orientée objet
SOLID
Duck Typing
Decouplage

Principe d’inversion des dépendances

Principe d’inversion des dépendances sur Wikipedia

Les modules de haut niveau ne devraient pas dépendre des implémentations de bas niveau.

Le cinquième des principes ‘SOLID’. Il énonce que les composants de hauts niveau ne devraient pas avoir à connaitre les détails de leurs dependences.

Prenons par exemple un programme qui lit des méta-donnés depuis un site web. Ce programme possède un composant principal qui connait un autre composant chargé de télécharger le contenu de la page, ainsi qu’un autre composant capable de lire les méta-donnés. En prenant en compte le principe d’inversion des dépendances, le composant principal ne devrait dépendre que de: un composant abstrait capable de télécharger des données binaires, ainsi que d’un composant abstrait capable de lire des méta-donnés depuis un flux binaire. Le composant principal ne devrais pas à connaitre les concepts de TCP/IP, HTTP, HTML, etc.

Ce principe est complexe étant donné qu’il semble ‘inverser’ les dépendances attendues dans un système (d’où le nom). En pratique cela veut aussi dire qu’un composant ‘orchestrateur’ doit s’assurer que les types abstraits soient correctement implémentés. (Pour reprendre l’exemple précédent, quelque chose doit fournir un downloader de fichier HTTP et un liseur de meta tag HTML au composant lisant les méta-donnés.) On touche alors à des patterns tels que l’inversion de contrôle et l’injection de dépendances.

Voir aussi :

Programmation orientée objet
SOLID
Inversion de contrôle
Injection de dépendances

Principe DRY

Principe DRY sur Wikipedia

Dans un système, toute connaissance doit avoir une représentation unique, non-ambiguë, faisant autorité.

DRY est un acronyme pour Don’t Repeat Yourself (ne vous répétez pas). Ce principe vise à aider les développeurs à réduire les répétitions de code et à garder l’information à un seul endroit. Il a été formulé en 1999 par Andrew Hunt et Dave Thomas dans le livre The Pragmatic Developer.

L’opposé de DRY serait WET (Write Everything Twice ou We Enjoy Typing, qu’on peut traduire par Tout écrire en double ou On aime taper au clavier).

En pratique, si vous avez la même information dans deux (ou plus) endroits, vous pouvez utiliser DRY pour les fusionner et réutiliser cette unique instance partout où c’est nécessaire.

Voir aussi :

The Pragmatic Developer

Principe KISS

KISS sur Wikipedia

Keep it simple, stupid. (Ne complique pas les choses)

Le principe KISS énonce que la plupart des systèmes fonctionnent mieux s’ils sont simples que compliqués. Par conséquent, la simplicité devrait être un but essentiel dans la conception et toute complexité inutile devrait être évité. Provenant de la marine Américaine en 1960, la phrase est attribuée à l’ingénieur Kelly Johnson.

Le principe est exemplifié le mieux par l’histoire de Johnson qui donna à une équipe d’ingénieurs une poignée d’outils et le défi de concevoir un avion de chasse qui soit réparable par un mécanicien lambda, sur le terrain, en condition de combat avec ces outils uniquement. Le “supid” fait donc référence à la relation entre la manière dont les choses cassent et la sophistication des outils à disposition pour les réparer, et non aux capacités des ingénieurs eux-mêmes.

Voir aussi :

Loi de Gall

YAGNI

YAGNI sur Wikipedia

Il s’agit d’un acronyme pour You Ain’t Gonna Need It. Que l’on peut traduire par: “vous n’en aurez pas besoin”.

Implémentez les choses uniquement quand vous en avez réellement besoin et non quand vous pensez que vous en aurez besoin plus tard. (Ron Jeffries) (Co-fondateur de XP et auteur du livre “Extreme Programming Installed”)

Ce principe d’Extreme Programming (XP) suggère que les développeurs ne devraient implémenter que les fonctionnalités qui sont nécessaires immédiatement et éviter de tenter de prédire l’avenir en implémentant des fonctionnalités qui pourraient être nécessaires plus tard.

Adhérer à ce principe devrait réduire la quantité de code inutilisé dans le codebase et permet d’éviter de passer du temps sur des fonctionnalités qui n’apportent rien.

Voir aussi :

À lire: Extreme Programming Installed

Illusions de l’informatique distribuée

Illusions de l’informatique distribuée sur Wikipedia

Aussi connues sous le nom de illusions de l’informatique en réseau, les illusions sont une liste de suppositions (ou croyances) concernant l’informatique distribuée, qui peuvent amener à des problèmes dans le développement logiciel. Les suppositions sont :

Le réseau est fiable
Le temps de latence est nul
La bande passante est infinie
Le réseau est sûr
La topologie du réseau ne change pas
Il y a un et un seul administrateur réseau
Le coût de transport est nul
Le réseau est homogène

Les quatre premiers éléments furent listés par Bill Joy et Tom Lyon vers 1991 et qualifiés pour la première fois d’“illusions de l’informatique distribuée” par James Gosling. L. Peter Deutsch ajouta les 5ème, 6ème et 7ème illusions. Gosling ajouta la 8ème illusion vers la fin des années 90.

Le groupe était inspiré par ce qui se passait à l’époque chez Sun Microsystems.

Ces illusions devraient être gardées à l’esprit pour concevoir du code résistant étant donné que chacune d’entre elle peut mener à une perception biaisée qui ne prend pas en compte la réalité et la complexité des systèmes distribués.

Voir aussi :

Traductions

Grâce à l’aide de merveilleux contributeurs, Hacker Laws est disponible dans plusieurs langues. N’hésitez pas à envisager de sponsoriser les modérateurs !

Langue	Moderateur	Status
🇧🇷 Brasileiro / Brésilien	Leonardo Costa
🇨🇳 中文 / Chinois	Steve Xu	Partiellement complète
🇩🇪 Deutsch / Allemand	Vikto
🇫🇷 Français / French	Kevin Bockelandt
🇬🇷 ελληνικά / Grecque	Panagiotis Gourgaris
🇮🇹 Italiano / Italien	Claudio Sparpaglione	Partiellement complète
🇰🇷 한국어 / Coréen	Doughnut	Partiellement complète
🇱🇻 Latviešu Valoda / Letton	Arturs Jansons
🇷🇺 Русская версия / Russe	Alena Batitskaya	Partiellement complète
🇪🇸 Castellano / Espagnol	Manuel Rubio (Sponsor)	Partiellement complète
🇹🇷 Türkçe / Turc	Umut Işık

Si vous souhaitez mettre à jour une traduction, vous pouvez ouvrir une pull request. Si vous voulez ajouter une nouvelle langue, connectez vous à GitLocalize pour créer un compte, puis créez une issue afin que je vous ajoute au projet ! Il serait également très apprécié d’ouvrir une pull request correspondante qui met à jour le tableau ci-dessus et la liste de liens au début de ce fichier.

Projets liés

Tip of the Day - Recevez quotidiennement une loi / principe.

Contribuer

N’hésitez pas à contribuer ! Vous pouvez créer une issue pour suggérer une addition ou un changement, ou ouvrir une pull request pour proposer vos propres modifications.

Merci de lire le guide de contribution pour connaitre les pré-requis concernant le style, le contenu, etc. Veuillez lire également le code de conduite afin de le respecter lors des discussions sur le projet.

TODO

Si vous êtes atteris ici vous avez cliqué sur un lien concernant un sujet qui n’a pas encore été rédigé. Désolé ! Tout n’est pas encore terminé.

N’hésitez pas à créer une issue pour avoir plus de détails, ou ouvrez une pull request pour soumettre votre propre texte sur le sujet.

This site is open source. Improve this page.

hacker-laws-website

💻📖 hacker-laws

Introduction

Lois

Loi d’Amdahl

Théorie de la vitre brisée

Loi de Brooks

Loi de Conway

Loi de Cunningham

Nombre de Dunbar

Loi de Gall

Loi de Goodhart

Rasoir de Hanlon

Loi de Hofstadter

Loi de Hutber

Cycle du hype & Loi d’Amara

Loi d’Hyrum (loi des interfaces implicites)

Loi de Kernighan

Loi de Metcalfe

Loi de Moore

Loi de Murphy / Loi de Sod

Rasoir d’Occam

Loi de Parkinson

Effet d’optimisation prématurée

Loi de Putt

Loi de Reed

Loi de la conservation de la complexité (Loi de Tesler)

Loi des abstractions qui fuient

Loi de futilité

Philosophie d’Unix

Modèle de Spotify

Loi de Wadler

Loi de Wheaton

Principes

Principe de Dilbert

Principe de Pareto (règle des 80/20)

Principe de Peter

Principe de robustesse (loi de Postel)

SOLID

Principe de responsabilité unique

Principe ouvert/fermé

Principe de substitution de Liskov

Principe de ségrégation des interfaces

Principe d’inversion des dépendances

Principe DRY

Principe KISS

YAGNI

Illusions de l’informatique distribuée

À lire

Traductions

Projets liés

Contribuer

TODO